Hi @Zonglei,
Thank you for reminding me!
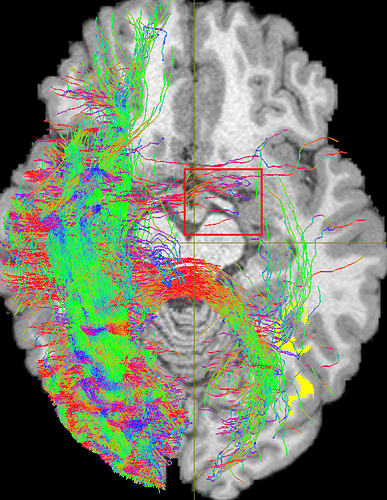
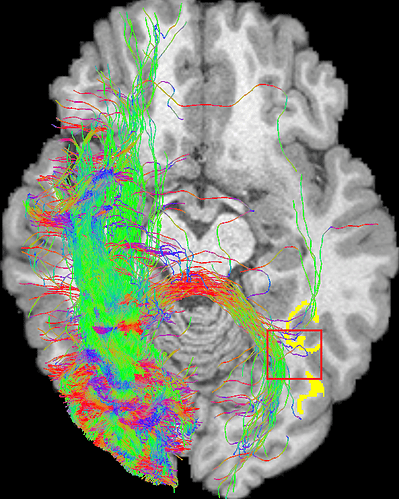
Yup, maybe the curvature radius is too small ever before, but the phenomenon still exists after I changed the angle from 45° (R=0.866mm) to 36° (R=1mm), even 24° (R=1.5mm):
-angle 36
-angle 24
I am very confused and hope to get the answer!
Jian