Hi again @olie, Octavian,
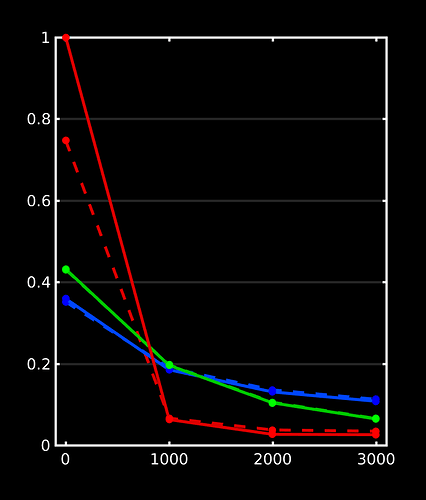
Great stuff, thanks for posting all that! It beautifully reproduces my findings up to now on a lot of datasets, as well as data from a few of other people around here who’ve also wondered about the differences. Let us take a look at how we can perfectly explain everything we see in your results. I did a quick plot of your reported response functions’ b-value dependent behaviour, which makes things a bit more visual (I always recommend taking a look at things like this):
WM-GM-CSF = blue-green-red (as in my abstracts, and also in Ben’s original MSMT-CSD paper), dhollander is full lines, msmt_5tt is dashed lines; horizontal axis is b-value (just 3 discrete points of course; your b-values); vertical axis is amplitude of each response (your numbers, but in general these are arbitrary units).
Ok, so, observations:
- WM responses are as good as the same
- CSF response function of
msmt_5tthas a drastically lower b=0 intensity (compared todhollander) and minor increase in b=700 intensity - GM response function of
msmt_5tthas a significantly larger b=0 intensity (compared todhollander) and minor increase in b=700 intensity.
What can have impacted msmt_5tt to explain the different CSF and GM responses?
- CSF:
- Mis-registration of T1 vs DWI data: since CSF has the largest b=0 of all tissues by a wide margin, any (even subtle) mis-registrations will cause selection of “CSF” voxels that are non-CSF tissues, resulting in what can only become a severe drop in b=0 versus what it should have been.
msmt_5tthas one additional form of protection, which is an additional FA threshold for GM and CSF (to stay below). This protects it a little bit against these problems where CSF interfaces with WM (high FA) specifically. However, it doesn’t protect against this issue at CSF-GM interfaces. And even at CSF-WM interfaces, it’s very limited in doing so, since “WM” FA drops very easily to quite low levels when even partial voluming only a bit with CSF. So we may still see (and get) voxels there with a low enough FA to make the cut, yet still significantly partial volumed by WM. - Mis-segmentation of tissues that aren’t 100% CSF as still very much close to “100% CSF”. Number one culprit to significantly cause this even in perfectly healthy brains: the choroid plexus structures in the ventricles. While these are sometimes barely decently visible in a T1 image, they are very real structures sitting there and changing the b=0 more than enough to be taken seriously. I note in your dataset, since you’ve also shown the 5tt image in the background (I presume) that in fact some of those got segmented as GM (which is also not what they are, see further on for GM response issues), which at least kept them partially away from the CSF selected voxels (one would hope).
- Mis-registration of T1 vs DWI data: since CSF has the largest b=0 of all tissues by a wide margin, any (even subtle) mis-registrations will cause selection of “CSF” voxels that are non-CSF tissues, resulting in what can only become a severe drop in b=0 versus what it should have been.
- GM:
- Mis-registration of T1 vs DWI data: you effectively run the opposite risk compared to the CSF scenario here. You could first assume that this may “average” a bit out in a way: GM is mostly the cortex, which is mostly wedged in between WM and CSF (outside the brain) areas, so some random mis-registration may naturally land you with some GM-segmentation still overlapping (in DWI space) with actual GM, but some also with WM and some with CSF. Let’s naively assume 33% for each tissue type ending up in the “GM” segmentation or something like that… you could then naively assume that this saves the day a bit, since the b=0 of GM also sits in between that of WM and CSF. However, 2 important biases come to ruin the day here: first, the CSF has a much much higher b=0 whereas WM only has a moderately smaller b=0 intensity, so an “average kind of” mis-registration already biases towards the higher b=0. Second, there’s that FA threshold for selecting CSF at the end too, which prevents those accidental inclusions of WM voxels. So the bias will almost uniquely be towards the b=0 of CSF, which is indeed drastically higher than it should be (for GM).
- Mis-segmentation of tissues that aren’t 100% GM, or not even GM at all: the cortex is not that wide, so the not quite 100% thing happens very easily. However, the “not even GM at all” is the biggest risk here: about any pathology of WM that lowers “fibre density”-like aspects, or even more so myelination, will result in a lower (than WM) T1w intensity. Think for instance WM hyperintensities in ageing or multiple sclerosis. We’ve got heaps of those over here (in our institute):
5ttgenclassifies a lot of that stuff as (almost pure even) GM. However, in practice, it’s often a mix of tissue changes that tend towards a higher b=0 (well, it’s T2 hyperintensities anyway, right) then what you’d even see in healthy GM. Furthermore in your case: there’s the choroid plexus again. Shouldn’t be GM, and at your DWI resolution of 2mm isotropic, it’s going to have lots of partial voluming from CSF. However, an overwhelming amount of your GM voxels will still come from the actual cortex, so the choroid plexus isn’t going to be responsible for much problems in your case.
In practice, for your example, I reckon both “mis-registration” scenarios have played out, and to a (much) lesser extent the "mis-segmentation ones. I note for instance also a band of “GM” segmented at the interface of the thalamus and the CSF. I can see how that could’ve come from the T1, although it’s wider then what I’d expect: maybe you had an anisotropic T1w resolution? Or the T1 was blurry otherwise? I’d expect to see a band like that, just not that wide. Again, the CSF’s T2 will overwhelm there, and bias your GM response towards CSF properties.
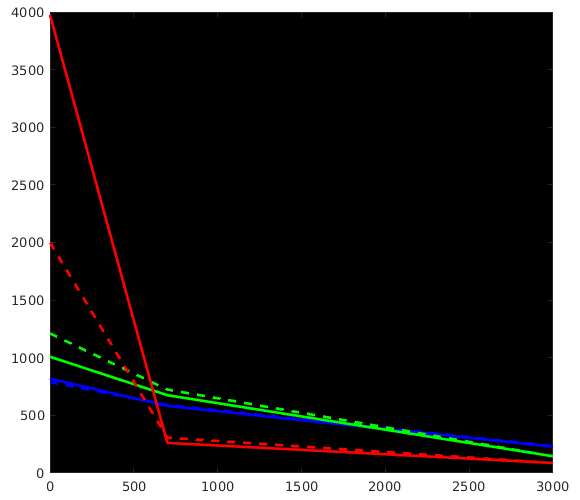
If you do nail registration as good as realistically possible (combined with the best image quality imaginable), you may be able to reduce msmt_5tt’s GM problems. Note they weren’t apparent in the data I presented in that abstract. I’ve also pushed this to high quality data, by using the preprocessed HCP data. I reason that’s quite up there in terms of data and preprocessing quality. See here the results of such a dataset:
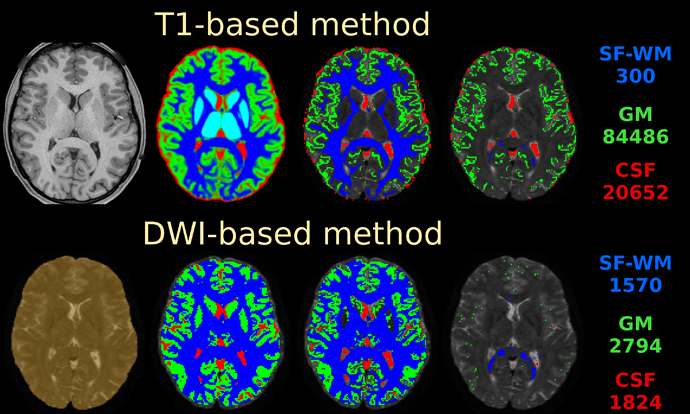
Top row is msmt_5tt going through some steps (final column is the final voxel selection in diffusion space), bottom row is dhollander going through the same “main” steps as presented in the abstract. These are the responses that came out here:
Note the WM and GM are basically the same between both algorithms (even though the selected numbers of voxels for those 2 tissues were very different; this is good news in general, it does show that in good conditions the 2 very independent strategies go to a consensus… reassuring!). Note that the CSF still suffers from the problem described in the abstract (and reproduced on the forums here already a couple of times by people, and by your data now as well). If we assume very good registration quality in the HCP case, then segmentation issues it is: note the final CSF voxel selection for msmt_5tt’s CSF is still quite generous, and indeed includes the choroid plexus and a lot of risky voxels at the edge of the mask. The dhollander algorithm is much more picky, and goes directly with the diffusion data’s properties (actually looking for a sharp decay as is expected for free diffusion). Look how it nicely avoids the choroid plexus and anything that even barely risks being partial volumed. But the dataset is so large, we can easily afford being this picky: we’ve still got 1824 CSF voxels (and lots of images per b-value) to work with. That should be more than enough to estimate just one average number for each b-value. After all, this is not about a segmentation to begin with: it’s about a very picky selection. (to see the full selection of voxels from dhollander for this HCP dataset in 3D, see the screen shot posted here)
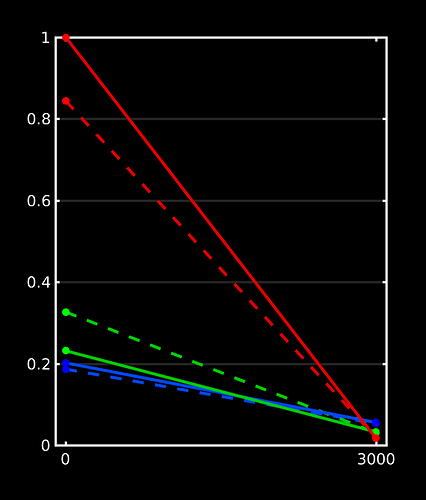
Here’s the responses I got over here on a dataset (with a more realistic spatial resolution), yet with some lesions:
I can’t disclose much of the other results on these datasets at this point, but essentially lesions got selected as GM by 5ttgen, and hence the GM response function selection by msmt_5tt came mostly from those areas. Note the now very expected CSF problem also pops up (of course, as always). There we’re also slight mis-registrations in place here, due to partially uncorrected EPI distortions (motion / eddy currents were corrected though). Again, everything with the expected effects on the response functions.
Next, consequences for your FOD estimation when using your responses. I’ll talk in terms of biases caused by the biased GM and CSF responses that resulted from msmt_5tt. To understand this, it’s useful to consider tissue interfaces, because that’s where the contrast between 2 tissues will go wonky if either (or both) responses aren’t appropriate for what they’re supposed to represent. Here’s all the interfaces:
- WM-CSF: troubles here caused by the underestimated CSF b=0, or in general underestimated CSF diffusivity. This scenario is mostly described in the original abstract. Essentially: more “CSF” is needed to represent the b=0 signal using the CSF response that has too little b=0. It’s actually more about b=0 versus the other b-values, and hence about the diffusivity, but the argument has the same format. The opposite holds for the WM response contribution here (even though the culprit is the CSF response, but it’s all about relative balance between both). Result: underestimation of your WM FOD, and it sometimes disappearing entirely for some levels of CSF partial voluming. Your responses and the resulting effect at the WM-CSF boundary is actually one of the most severe I’ve every seen. Don’t underestimate the impact for subsequent applications: e.g. the midbody of the corpus callosum (that is already quite a thin structure relative to DWI resolutions) is impacted severely, on both sides, so it grows significantly “thinner”. This impact quantification of FD, FC and FDC for this structure, and may cause strong biases in any connectome (as a significant number of the left-right connections of the brain go through this crucial bridge). Furthermore, in pathology (e.g. lesions), this may overestimate the free water content, and sometimes severely underestimate the amount of healthy intra-axonal space left. Pretty risky if e.g. surgery is informed by that.
- WM-GM: troubles due to overestimated GM b=0. The (or a) simple(st) way to reason about this is to think of the GM response having become a bit more CSF-like. So the behaviour at the cortex becomes a little bit more like the scenario where we would have no GM response (i.e. 2-tissue CSD with WM and CSF). So essentially, some isotropic GM signal that would otherwise be captured by the GM response, is now not. And too much signal ends up in the WM compartment, which is your WM FOD. You can see this, as you’ve described, by larger FODs there… but note that in most cases in your more detailed zoomed screen shots, you can observe that these are messy FODs, or messy additions to FODs that were cleaner in the
dhollandercase. This is the “fingerprint” of isotropic signal being deconvolved by an anisotropic WM response, while using an SH basis that is cut off at a certain lmax. If you deconvolve perfectly isotropic signal that has just a tiny, tiny bit of noise on it with an anisotropic WM response, you don’t get a nice isotropic FOD, but a sphere full of random peaks. The noise is sharpened, and the SH result goes up and down like crazy. Not a useful addition to your WM FOD in those regions, that is… Again in case of pathology (again e.g. lesions), this may underestimate e.g. gliosis, and have some of its effects messing with your WM FODs. You also end up overestimating AFD then in these regions, and hence underestimate some of the damage in case of a genuine lesion. - GM-CSF: we can’t see this going with just your WM FOD; the GM and CSF outcome maps may show some effects here (in addition to those at the other interfaces described above). But both GM and CSF responses are biased towards each other… so you may see a (false) over-contrast of the GM-CSF spectrum. It’s as if you set the windowing on an image too tight in a way. The balance may also be disturbed dependent on which bias (of both responses) “wins out”. In pathology… well, this becomes a mess.
Finally, note that in general both of these GM and CSF response function biases strictly reduce the range of signals you can fit (even independent of meaning and interpretation). See for instance Figure 5 in this recent abstract: the triangle in the right hand side schematic will strictly shrink due to either of those biases. This schematic has actually already helped me a lot to translate formal observations about the response functions as well as 3-tissue CSD into visual interpretations, and more intuitive explanations. Using that schematic, you can perfectly obtain the above explanations at tissue boundaries under the presence of a response function bias as well. It’s a mighty handy tool (if I say so myself 
) for white board discussion marathons (and my boss/supervisor has a big one in his office, so fun times guaranteed 
). Also, both the inner workings of my SS3T-CSD as well as even the strategy of the dhollander algorithm can be made very visual on that actual schematic.
Alright, if I continue like this, I may end up with the actual paper almost written. 
I’ll briefly get to your questions, so I don’t overlook anything you were looking for:
This should now be clear from the above. Especially important for e.g. corpus callosum and fornix.
So from the above: be very careful about this, as a lot of this seems to be “false positive signal” that shouldn’t have ended up in the WM FOD, but rather in the GM compartment. Some of in in your zoomed screen shot is particularly messy, and also quite big compared to the actual nearby deeper WM. Not surprising: if this signal now ends up in the WM FOD, but has to be modelled by the WM response’s lower b=0 value, it’s going to be over-represented even more.
Even though both GM and CSF response biases of msmt_5tt work together in your case to give you this appearance (of dhollander versus the biased msmt_5tt), this isn’t a representation of both of them being more suited towards a certain region. Bigger FODs aren’t always better, as we’ve seen from our WM-GM boundary reasoning.
This is somewhat unrelated to all of the above. First things first: at the moment dhollander uses tournier internally for the final single-fibre WM selection, but dhollander already narrows things down for tournier to a safer selection of WM (both single-fibre as well as crossings and other geometries still). dhollander also determines a more relative number of voxels (compared to WM size and resolution) that scales better in case of pathologies or varying spatial resolutions, and then asks tournier for that. tournier out of the box (default) always goes for 300 voxels, independent of anything. You can set this number yourself of course as well if you run tournier. But in general, the core of the strategy to identify the single-fibre voxels is the same. In practice, for a single-shell response they also tend to give a very similar result. For multi-shell purposes though, tournier ignores lower (and b=0) b-values. dhollander has a sneaky outlier-rejection going on to avoid pesky CSF-partial volumed voxels and other unexpected T2 hyperintensities. This does help it to get slightly better multi-shell (or even b=0 and single-shell) response for WM. But this doesn’t matter for single-shell single-tissue CSD: for that one, only the shape of the response is the crucial thing. No drastic differences here. I’d advise to simply run tournier directly if you need a single-shell single-tissue CSD response. No need to overcomplicate things for that scenario. In the future, there is a chance that I change what dhollander does at this stage. It’ll always be inspired by the general strategy of tournier though, but there’s a few other things of concern going on, and an opportunity to slightly improve the multi-shell (or b=0 + single-shell) WM response; but I need to figure out if I can get it ultimately robust. (robustness is a property of the dhollander algorithm that I’d personally never want to sacrifice)
At the moment, the default for all algorithms will inherently end up being lmax=10. That is, for all WM responses (GM and CSF have lmax=0) and only for the non-b=0 shells of that WM response (again, b=0 has lmax=0). See some experiments and discussions and equally lengthy stand-alone posts on this: here, here and here are some relevant bits, but happily read that entire page of discussion (they’re all bits on the same page). If you’ve got any further questions on that front, don’t hesitate to ask for clarification. But the gist is: even with crappy 12 direction data (imagine that), and even with only 100 voxels for the single-fibre WM response (that’s a lot less than what you’d realistically always get), you’ve still got 1200 measurements, to estimate just 6 parameters (that’s the lmax=10 response model, i.e. lmax=10 for a zonal spherical harmonic basis). On top of that, we’ve got non-negativity constraints and monotonicity constrains for the WM response (if those 1200 measurements weren’t already enough to estimate just 6 parameters). And lmax=10 is certainly more than flexible enough to represent responses up to b=5000 in vivo. So it’s flexible enough, and mighty safe given the massive amounts of data we always have for this task.
As mentioned above, even a perfect registration doesn’t overcome all issues. But for it to at least be as perfect as possible, you’d need it to be sub-voxel accurate (relative to the DWI spatial resolution). And of course, up to that same level of accuracy, be able to overcome the many distortions that plague EPI data. And even then still, msmt_5tt will trip up over mis-segmentations… all while the actual information about the actual responses you’re after is actually right there in the DWI data, rather than in a T1. Note that the msmt_5tt algorithm was never meant to be the ultimate way of doing things; but at the time there was certainly need for at least some automated need to do this. It would otherwise have sounded very arbitrary in the paper(s) that we picked our responses “manually”… it also wouldn’t have been very convenient in practice to do this on cohorts of many tens or hundreds of subjects. msmt_5tt certainly did what it needed to do at the time. However, your question (about registration) remains important: for tasks like ACT, you still want that registration to be as good as it can get of course. It may be worthwhile asking that one specifically again in its own topic (with a well chosen title) to get some input from other peoples’ experience. I’ve seen a few different things here an there on the forum before too.
I should have read all question before I started typing above. 
So, as mentioned in the other answer: it’s also 10.
Yep, no worries, as mentioned in that other answer above. You’d even get away with 12 directions (or less!). However, the question you’ve got to ask for such a pipeline is what lmax for the CSD step is till appropriate, or even if the CSD step itself is still reasonable. But the response function estimation is (un)surprisingly safe. Also be careful with the results of such a pipeline on data with such differing qualities, as in: don’t compare such results with each other (i.e. based on different qualities relative to each other).
Looks like I almost wrote it in this post now. But other than that: it is my first and foremost priority at the moment, even before any SS3T-CSD shenanigans. Other projects (well, collaborations) do run in parallel, but those are now bootstrapped sufficiently (I hope). Time to focus on this one; lock myself up without internet and with a typewriter.
Again, very useful as a topic of its own; I expect different experiences in the wider MRtrix3 community. I’m always happy to learn what people do for these steps as well!
Cheers,
Thijs