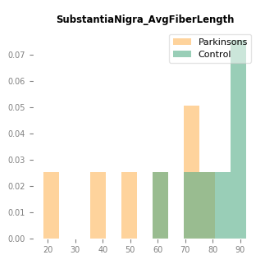
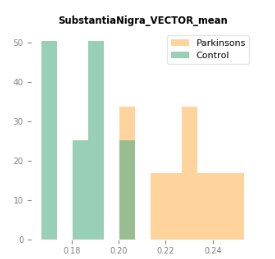
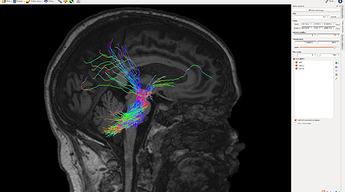
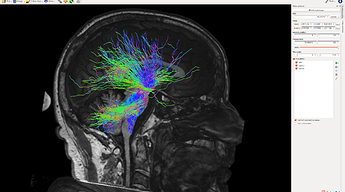
With such consistent results, is it reasonable to say the fiber tracking results could be acceptable even without the quantitative benefits that SIFT provides in this case?
Depends on what you mean by “acceptable”. Even if you would be able to obtain a “difference” (whether subjectively obvious or statistically significant) without the use of SIFT, you would still have the limitations in both interpretation and likelihood of journal reviewer approval that come with counting streamlines. There’s also the higher-level scientific question of whether you’re looking at data both with and without SIFT and choosing which to present, which, unless you are using these data to inform a subsequent study, brings with it the issues of cherry-picking / multiple comparisons.
Cause I’m considering to produce more data with such a procedure and without SIFT may be faster.
Sounds like I went to all the effort of creating and publising SIFT2 for nothing 
First, tensor2metric -vector vectimage.nii.gz has been applied for generating the principal vector images, rather than all three components.
Be aware that by default, tensor2metric -vector will generate an image that is modulated by FA, ie. are not unit vectors that represent orientation information only. You can disable this using the -modulate option.
Second, tcksample was used to extract the direction information from the principal vectors, with vectimage.nii.gz as input images and the output scatter values.
For the sake of this explanation, let’s imagine that you are not using tcksample to obtain point samples at the vertices of streamlines. Instead, you are doing more of a VBA-type analysis, where you are warping all subject image data toward a central template space; then, within a specific location in that template space, comparing the underlying values across subjects. Such a comparison across subjects would only make sense if, for two different subjects where the fibre bundle follows precisely the same trajectory, there is no difference in the underlying image values. Now consider the two following possibilities:
-
The tensor glyphs could be near-identical between the two subjects, but for whatever numerical reason, the direction of the first eigenvector is precisely reversed in the second subject with respect to the first. The estimated direction of the underlying fibres is the same due to the antipodal symmetry of the diffusion signal; yet in your analysis framework, the underlying image values could not be any more different.
-
Imagine two subjects that position themselves in the scanner at considerably different angles to one another, such that the alignment of the anatomical bundle relative to the scanner axes differs substantially. If, during transformation of their image data to template space, you did not appropriately realign the underlying orientation information (whether diffusion gradient table, diffusion tensors, eigenvector orientations, …), then again, the underlying image values containing the X, Y, Z components of the first eigenvector relative to the scanner axes will differ substantially even if the two subjects are identical.
Sampling these image intensities via tcksample does not mitigate either of these issues. Even if not using image transformation / registration, the fact that the subject anatomy may be aligned to the scanner axes differently between subjects must be appropriately taken into account; as must the antipodal symmetry of fibre orientations.
I guess it may help identify axial and radial diffusivities.
Why not just extract the axial and radial diffusivities?
Fixel images may better describe directions, I didn’t test it though.
Fixel orientations are encoded as XYZ triplets relative to the image axes, just as the first eigenvector via tensor2metric -vector is. While the former enables the representation of more than one fibre orientation in each voxel, the issues described above still apply.
All of the above is not to say that it is not possible to perform some kind of comparison across subjects in terms of fibre orientation; only that to do so would require tailored analysis methods to do so robustly.