Hi,
I am getting an error in the eddy command of the dwipreprocessing. I am using FSL 5.0.9 with eddy patch. I am using the SGE Cluster.
The command I use is as follows:
dwipreproc -pe_dir AP DWI_denois.mif DWI_denois_preproc.mif -rpe_none $quiet -nthreads ${NSLOTS} $force -eddy_options "--data_is_shelled "
The force and quiet are flags for overwriting warning.
The error message is as follows:
dwipreproc: e[00;31m[WARNING] Total readout time not provided at command-line; assuming sane default of 0.1e[0m
e[03;36mCommand:e[0m mrinfo dwi.mif -export_grad_mrtrix grad.b
e[03;36mCommand:e[0m dwi2mask dwi.mif - | maskfilter - dilate - | mrconvert - mask.nii -datatype float32 -stride -1,+2,+3
dwipreproc: e[03;32me[0m
dwipreproc: e[01;31m[ERROR] Command failed: dwi2mask dwi.mif - | maskfilter - dilate - | mrconvert - mask.nii -datatype float32 -stride -1,+2,+3e[0me[03;34m (dwipreproc:457)e[0m
dwipreproc: e[03;32mOutput of failed command:e[0m
dwi2mask: [ERROR] DWI volumes could not be classified into b-value shells; gradient encoding may not represent a HARDI sequence
The dwi2mask command fails.
Could you please advise what could be the issue?
Thank you.
Apoorva
Seems like you have an exotic DW encoding… What does this report:
mrinfo DWI_denois.mif -shells -shellcount
I’d expect that would probably give rise to the same DWI volumes could not be classified into b-value shells error… Assuming it does, you can drill into the specific of your encoding with:
mrinfo DWI_denois.mif -dwgrad
which will give you the DW encoding as MRtrix3 interprets it (you can get the original unmodified encoding by adding the -raw_dwgrad option to the above - this skips the unit normalisation and scaling by gradient vector norm - see here for details).
Hi,
The ‘mrinfo DWI_denois.mif -shells -shellcount command’ indeed gives the error you specified.
mrinfo DWI_denois.mif -shells -shellcount
mrinfo: [ERROR] DWI volumes could not be classified into b-value shells; gradient encoding may not represent a HARDI sequence
The $ mrinfo DWI_denois.mif -dwgrad command gives the following output:
-0.57735 0.57735 0.57735 5
-0.57735 0.57735 0.57735 5
0.999682 0.0201575 -0.0151623 200
0.00032054 0.602889 0.797825 4985
-0.00507475 -0.0102284 0.999935 200
-0.00011974 -0.802913 -0.596096 4985
-0.710691 -0.0108116 0.703422 395
4.8e-07 -0.999997 -0.00239615 5010
0.701825 -0.712272 -0.0104731 405
0.600888 0.00298427 0.799328 4965
5.895e-05 -0.718672 -0.69535 400
-0.598494 -0.801124 -0.00243904 5005
0.577008 0.585676 0.569249 599.999
0.800963 0.00306244 0.598706 4970
0.577008 -0.585676 0.569249 599.999
-0.798487 -0.602007 -0.00228192 5000
7.64e-06 -0.999981 -0.00618013 810
0.407565 -0.818365 0.405178 4795
0.891448 0.453086 -0.0058056 1005
0.408289 -0.411625 0.814779 4775
0.896478 0.00723177 0.44303 995.001
0.408289 0.411625 0.814779 4775
-0.444725 -0.895649 -0.00576262 1010
-0.407874 -0.818903 -0.403777 4790
0.448482 0.0063503 0.893769 989.999
0.816234 -0.411277 0.405725 4785
-0.00043871 -0.897969 0.440059 1005
0.816234 0.411277 0.405725 4785
-0.0004406 -0.453876 0.891065 995
0.426028 -0.642492 0.636949 4390
-0.816017 -0.414494 0.402878 1200
0.426028 0.642492 0.636949 4390
0.81714 -0.414907 -0.400169 1195
0.638897 -0.64225 0.423469 4395
-0.40711 -0.820321 0.401666 1205
0.639582 -0.429733 0.637388 4385
-0.408588 -0.414752 0.813041 1195
0.639582 0.429733 0.637388 4385
0.409509 -0.415708 -0.81209 1190
0.638897 0.64225 0.423469 4395
0.407721 -0.82156 -0.398501 1205
0.217856 -0.874644 0.433056 4200
-0.704232 -0.709956 -0.00440404 1610
0.218178 -0.440011 0.871085 4180
0.708885 0.00536232 0.705303 1585
0.218178 0.440011 0.871085 4180
-0.00044024 -0.711749 0.702434 1600
-0.218003 -0.87534 -0.431573 4195
0.999977 0.00558527 -0.00391128 1795
0.435372 -0.874172 0.215114 4205
0.665193 0.670564 0.328425 1805
0.436821 -0.221681 0.871806 4175
0.667175 0.338713 0.663439 1795
0.436821 0.221681 0.871806 4175
0.667175 -0.338713 0.663439 1795
-0.435564 -0.874506 -0.213362 4200
0.665193 -0.670564 0.328425 1805
0.872053 -0.43944 0.215446 4190
0.333041 0.671278 0.66217 1800
0.87319 -0.221654 0.43406 4180
0.333041 -0.671278 0.66217 1800
0.87319 0.221654 0.43406 4180
-0.00112104 -0.00449361 0.999989 1785
0.872053 0.43944 0.215446 4190
0.950523 0.00510864 -0.310613 1985
0.00044888 0.450809 0.89262 3980
0.947113 -0.320878 -0.00380253 2000
-0.00011084 -0.896881 -0.442273 3995
-0.316659 -0.00447619 0.948529 1980
0.445827 -0.895115 -0.00279058 4010
0.315046 -0.949069 -0.00377631 2010
-0.447889 -0.00327192 0.894083 3970
-0.00015447 -0.951028 -0.309104 2005
0.893009 -0.450032 -0.00257576 3995
0.00079282 0.320958 0.947093 1990
0.896108 0.00349674 -0.443823 3970
0.904181 0.30621 0.297812 2195
0.229176 -0.691219 0.685343 3790
0.904181 -0.30621 0.297812 2195
-0.229482 -0.692145 -0.684305 3780
-0.300922 -0.907001 -0.294612 2205
0.68695 -0.690576 0.226283 3800
0.301662 0.306217 0.902902 2185
0.688755 -0.23309 0.686503 3780
0.301662 -0.306217 0.902902 2185
0.688755 0.23309 0.686503 3780
0.300738 -0.906314 0.296904 2205
-0.687243 -0.690872 -0.224482 3795
0.57694 0.581527 0.573556 2395
-0.00019651 -0.71105 -0.703141 3585
0.57694 -0.581527 0.573556 2395
0.235135 -0.943805 0.232256 3605
0.834427 0.00431612 -0.551102 2575
0.235827 -0.239389 0.941849 3575
0.829939 -0.557844 -0.00330685 2605
0.235827 0.239389 0.941849 3575
-0.555716 -0.00409388 0.831362 2580
-0.235231 -0.944256 -0.230318 3605
0.552757 -0.833336 -0.00329815 2610
0.705237 -0.708967 -0.00274865 3605
-0.00021195 -0.835789 -0.549051 2595
-0.708192 -0.00356633 0.706011 3575
0.00064112 0.558753 0.829334 2590
0.942595 -0.239331 0.232886 3590
0.800598 0.538068 0.263676 2800
0.942595 0.239331 0.232886 3590
0.802172 0.271552 0.53177 2790
0.00050161 0.246239 0.969209 3380
0.802172 -0.271552 0.53177 2790
-6.97e-05 -0.971499 -0.237043 3405
0.800598 -0.538068 0.263676 2800
0.241798 -0.970322 -0.00305879 3410
-0.533543 -0.804374 -0.261372 2800
-0.242789 -0.00345739 0.970073 3370
0.534972 0.271524 0.80005 2785
0.484416 -0.730375 0.481554 3395
0.534972 -0.271524 0.80005 2785
0.485022 -0.488821 0.725126 3385
0.533223 -0.803935 0.263366 2805
0.485022 0.488821 0.725126 3385
-0.267129 -0.805497 -0.528977 2795
-0.484891 -0.731024 -0.480089 3390
0.267171 0.538561 0.799107 2790
0.72722 -0.488681 0.482018 3390
0.267171 -0.538561 0.799107 2790
0.72722 0.488681 0.482018 3390
0.266884 -0.804567 0.530513 2800
0.969227 -0.246152 -0.0027906 3395
9.7e-07 -0.999995 -0.00311522 3215
0.971274 0.00388091 -0.237931 3380
0.969227 0.246152 -0.0027906 3395
-0.00063001 -0.00347089 0.999994 3175
0.970786 0.00387629 0.239914 3385
0.999988 0.00408237 -0.00282692 3190
-0.72722 -0.488681 0.482018 3390
0.267129 -0.805497 -0.528977 2795
0.727865 -0.489165 -0.480552 3385
0.267541 -0.539603 -0.798279 2780
-0.484416 -0.730375 0.481554 3395
-0.267171 -0.538561 0.799107 2790
-0.485022 -0.488821 0.725126 3385
-0.266884 -0.804567 0.530513 2800
0.485742 -0.489552 -0.72415 3380
0.533543 -0.804374 -0.261372 2800
0.484891 -0.731024 -0.480089 3390
-0.534972 0.271524 0.80005 2785
-0.241798 -0.970322 -0.00305879 3410
-0.534972 -0.271524 0.80005 2785
0.242789 0.00345739 0.970073 3370
-0.533223 -0.803935 0.263366 2805
-7.021e-05 -0.971016 0.239013 3410
0.801114 -0.538356 -0.261512 2795
-0.00050161 -0.246239 0.969209 3380
0.803103 -0.271809 -0.530231 2780
0.943048 0.239432 -0.230939 3585
-0.802172 -0.271552 0.53177 2790
0.943048 -0.239432 -0.230939 3585
-0.800598 -0.538068 0.263676 2800
-0.705237 -0.708967 -0.00274865 3605
-0.00064112 -0.558753 0.829334 2590
0.708192 0.00356633 0.706011 3575
-0.00021202 -0.834785 0.550576 2600
-0.235135 -0.943805 0.232256 3605
0.555716 0.00409388 0.831362 2580
-0.235827 -0.239389 0.941849 3575
-0.552757 -0.833336 -0.00329815 2610
-0.235827 0.239389 0.941849 3575
0.833415 0.0043044 0.55263 2585
0.235231 -0.944256 -0.230318 3605
-0.829939 -0.557844 -0.00330685 2605
-0.00039238 -0.710056 0.704145 3595
0.57766 -0.582258 -0.572088 2390
-0.68695 -0.690576 0.226283 3800
-0.57694 -0.581527 0.573556 2395
-0.688755 -0.23309 0.686503 3780
0.300922 -0.907001 -0.294612 2205
0.689687 -0.23335 -0.685478 3770
-0.301662 0.306217 0.902902 2185
0.687243 -0.690872 -0.224482 3795
-0.301662 -0.306217 0.902902 2185
-0.229176 -0.691219 0.685343 3790
-0.300738 -0.906314 0.296904 2205
0.229482 -0.692145 -0.684305 3780
0.904871 -0.306404 -0.295508 2190
0.893009 0.450032 -0.00257576 3995
0.904871 0.306404 -0.295508 2190
0.895433 0.003491 0.445182 3975
-0.00079282 -0.320958 0.947093 1990
-0.445827 -0.895115 -0.00279058 4010
-0.00015538 -0.950265 0.311442 2010
0.447889 0.00327192 0.894083 3970
0.316659 0.00447619 0.948529 1980
-0.00011103 -0.896144 0.443763 4000
-0.315046 -0.949069 -0.00377631 2010
-0.00044888 -0.450809 0.89262 3980
0.94975 0.00509873 0.312969 1990
-0.872053 -0.43944 0.215446 4190
0.947113 0.320878 -0.00380253 2000
-0.87319 -0.221654 0.43406 4180
2.14e-06 -0.999993 -0.00386732 1815
0.873834 -0.221769 -0.432703 4175
0.333453 -0.672487 -0.660735 1790
0.872425 -0.439604 -0.213594 4190.01
-0.333041 -0.671278 0.66217 1800
-0.435372 -0.874172 0.215114 4205
0.665899 -0.671099 -0.32589 1800
-0.436821 -0.221681 0.871806 4175
0.668377 -0.339147 -0.662006 1785
-0.436821 0.221681 0.871806 4175
-0.667175 -0.338713 0.663439 1795
0.435564 -0.874506 -0.213362 4200
-0.665193 -0.670564 0.328425 1805
-0.217856 -0.874644 0.433056 4200
-0.00044103 -0.713092 -0.701071 1595
-0.218178 -0.440011 0.871085 4180
0.704232 -0.709956 -0.00440404 1610
-0.218178 0.440011 0.871085 4180
-0.708885 -0.00536232 0.705303 1585
0.218003 -0.87534 -0.431573 4195
0.40711 -0.820321 0.401666 1205
-0.638897 -0.64225 0.423469 4395
0.408588 -0.414752 0.813041 1195
-0.639582 -0.429733 0.637388 4385
0.408588 0.414752 0.813041 1195
0.640285 -0.430257 -0.636328 4375
-0.407721 -0.82156 -0.398501 1205
0.639362 -0.642719 -0.422054 4385
0.816017 -0.414494 0.402878 1200
-0.426028 -0.642492 0.636949 4390
0.816017 0.414494 0.402878 1200
0.426623 -0.643175 -0.635861 4380
0.0004406 0.453876 0.891065 995
-0.816234 -0.411277 0.405725 4785
-0.00043707 -0.899567 -0.436783 1005
0.816743 -0.411536 -0.404437 4780
0.444725 -0.895649 -0.00576262 1010
-0.407565 -0.818365 0.405178 4795
-0.448482 -0.0063503 0.893769 989.999
-0.408289 -0.411625 0.814779 4775
0.891448 -0.453086 -0.0058056 1005
0.408917 -0.412091 -0.814228 4765
0.897827 0.00725749 -0.440289 990
0.407874 -0.818903 -0.403777 4790
-0.00126091 -0.00634322 0.999979 790
0.999992 0.00321519 -0.00241168 4980
0.999941 0.00880033 -0.00629136 800.001
0.801781 0.00306921 -0.59761 4960
0.578607 -0.587327 -0.565916 600
0.798487 -0.602007 -0.00228192 5000
-0.577008 -0.585676 0.569249 599.999
-0.600888 -0.00298427 0.799328 4965
4.451e-05 -0.715932 0.69817 405
0.598494 -0.801124 -0.00243904 5005
0.710691 0.0108116 0.703422 395
-0.00023942 -0.802098 0.597193 4995
-0.701825 -0.712272 -0.0104731 405
-0.00032054 -0.602889 0.797825 4985
0.00494776 -0.99988 -0.014653 210
I interpret the columns to be in the [ x y z b ] format.
The unmodified encoding command $ mrinfo DWI_denois.mif -raw_dwgrad gives the following result:
Image: "DWI_denois.mif"
************************************************
Dimensions: 144 x 144 x 87 x 258
Voxel size: 1.79861 x 1.79861 x 1.8 x 4.3
Data strides: [ -2 3 4 1 ]
Format: MRtrix
Data type: 32 bit float (little endian)
Intensity scaling: offset = 0, multiplier = 1
Transform: 1 0 -0 -124.1
0 1 -0 -114.3
-0 0 1 -78.69
comments: TE=1e+02;Time=114950.477;phase=1;dwell=0.330
dw_scheme: -0.57735,0.57735,0.57735,5
[258 entries] -0.57735,0.57735,0.57735,5
...
-0.00032054,-0.602889,0.797825,4985
0.00494776,-0.99988,-0.014653,210
mrtrix_version: 3.0_RC1-83-gc16a3d0e
After reading the documentation, should I import the DW table in the FSL format?
Could you advise how to interpret the information in the mrinfo?
Thank you.
Apoorva
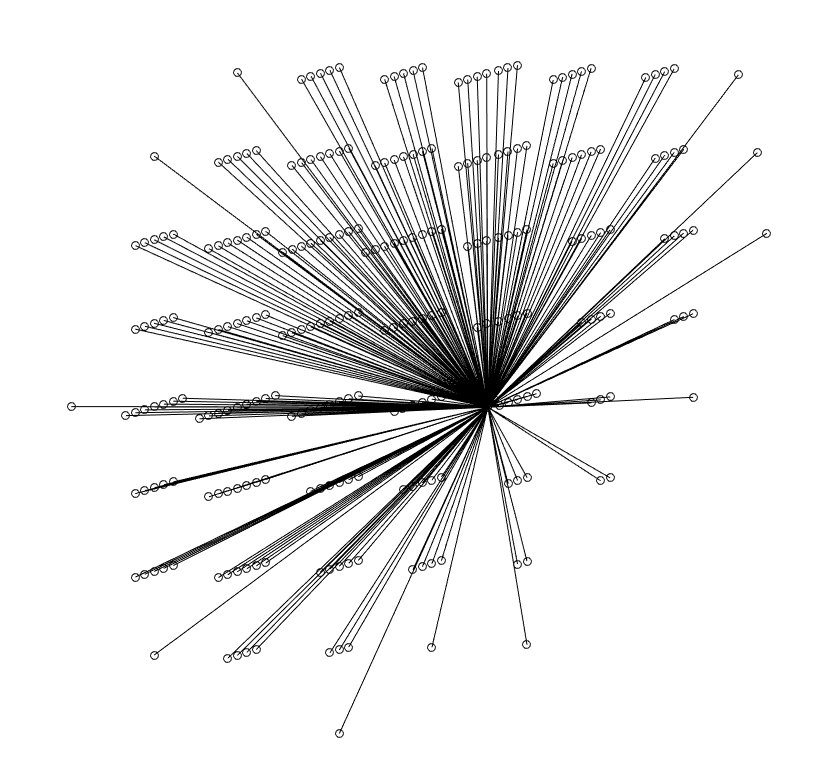
Well, the error message was spot on: your acquisition looks like it’s using a Diffusion Spectrum Imaging scheme, not a HARDI scheme - it’s acquired on a regular grid in q-space, it’s not multi-shell. Here’s what it looks like plotted in Matlab:
Unfortunately, we don’t offer any means of processing these types of data currently - other than the standard DTI pipeline. There’s not a lot we can do about this in the near future unfortunately…
Hi,
Could you please point me out to the standard DTI pipeline used by MRtrix?
I think I will have to process the DSI data through that pipeline.
Thank you so much for all your help on this!
Best,
Apoorva
Well, we don’t really have a standard pipeline for DTI analysis - MRtrix3 is almost entirely geared towards higher-order analyses. While you can do some analysis of the data, it’ll be limited essentially to dwi2tensor and tensor2metric. Preprocessing-wise, dwidenoise and mrdegibbs should work fine, but dwipreproc relies on the data being multi-shell, so you won’t be able to perform correction for motion, eddy-current distortion, and eddy-current distortions.
For these reasons, I’d recommend using other packages if you have to process these data, I’m sure there must a few good ones out there designed to handle DSI data - maybe other users on this forum can provide helpful suggestions…?
Thank you so much for all your help on this! I will use another software to perform motion correction and eddy current distortion correction before using MRtrix again for the steps ahead.
Apoorva