Dear experts
I have a multishell data set consisting of 6 b0,16 b700,30 b1200 and 50 b2800.
I was wondering about the best -lmax setting for dwi2response (in the case of dhollander or msmt_csd) and dwi2fod.
Peace,
Hamed
P.S. DWI Data has been denoised, unringed, eddy/epi, bias field corrected. T1 has been rigidly registered to DWIs and 5TT fsl has been generated.
Dear Hamed,
You can just go with the defaults (that means, don’t specify lmax at all). For your data, this will result in lmax=8 WM fODFs and lmax=0 CSF and GM fODFs (as these are isotropic compartments).
Cheers,
Ben
Thanks Ben,
And the choice of dhollander or msmt_csd for this data set?
Cheers,
Hamed
Hi @Hamed,
I second Ben: for that kind of data, the defaults will automatically work well for you; so no -lmax option needed for either dwi2response (dhollander as well as msmt_csd) or dwi2fod steps. dwi2response will give you lmax=0 response functions for GM and CSF, and lmax=10 response functions for the non-b=0 parts of the WM response. Feeding these responses to dwi2fod, combined with your data at hand, will (as Ben said as well) result in lmax=8 WM FODs and lmax=0 GM and CSF results. In practice, you don’t even have to check this (but you can, of course): the FODs will just behave as expected for any further uses (be it tractography, quantitative analysis, etc…).
As to choice of response function selection algorithm, I’m very confident dhollander will perform best if you’re looking at developed human data. So unless there’s anything particularly exotic about your data, dhollander should provide the most accurate result (furthermore with the least hassle). If things do start to get exotic on whatever front, it’s often very likely msmt_5tt will start to fail earlier, at least if running from 5ttgen fsl results out of the box on such data. Let us know if you run into any issues. If you want to be sure, simply copy-paste the contents of the response function files you get along with a screenshot or two of your WM FOD outcome; I’ll happily let you know if anything looks suspicious! 
Cheers,
Thijs
Hi Thijs
Thanks for the explanation.
Here is the outcome of applying your algorithm to the intensity normalized DWIs (across all subjects using dwiintensitynorm) for a sample of 30 Young Adults (YA) and 27 Old Adults (OA):
1) OA example:
WM response:
3558.514267251221 0 0 0 0 0
2098.960405698456 -562.8884179939862 87.42229861510899 -16.1008943696647 -3.404349856291478 -27.54914734197291
1631.736727070469 -664.1430944400951 174.9579915869785 -29.85632571483947 5.156498720614587 2.389530365950526
976.6217962898037 -598.9877074581515 285.7765430076679 -103.2611435214982 27.78032538379087 -4.09857207357174
CSF response:
16665.87786826252
1628.787969076357
382.6316718400435
109.395486221678
GM response:
4904.964072158946
2399.917058262798
1647.274519987118
657.1604089131876
1) YA example:
WM response:
3686.198042680062 0 0 0 0 0
2204.967027951133 -553.4787650069316 66.02828713310667 -10.51178782827822 -0.9376398524498114 -14.61632118314774
1698.439514893548 -658.2545210184219 149.9362405403081 -26.84502975330937 5.084326700209281 -0.9259074351671007
1019.055173983989 -621.7368580808204 267.9919349050045 -82.81758720253806 16.47263607548521 -4.149395477210142
CSF response:
15390.44616089431
1780.179435284597
381.0021403728388
63.85700740204156
GM response:
4892.806584867702
2585.051176312267
1807.91729561205
727.2326239360207
Average across all subjects:
WM response:
3673,78246518564 0 0 0 0 0
2187,96829458079 -581,806313823357 82,9272268496216 -10,0882006049367 -1,62410147212965 2,33733880521584
1669,43229520527 -689,944617246396 170,043848731565 -28,7063852687714 3,53444622956215 -2,20799462390421
1011,47705505164 -641,201831299893 293,104616514553 -98,9208818298173 24,7964657673854 -5,90174651986964
CSF response:
16151,2721783807
1423,64195274047
367,704621584411
128,759910841613
GM response:
4844,38733085823
2508,82026184851
1738,23882951545
687,026390155180
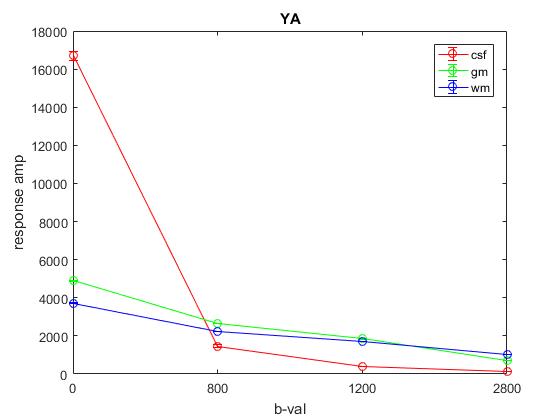
Plot of average response (1st column) across YA:
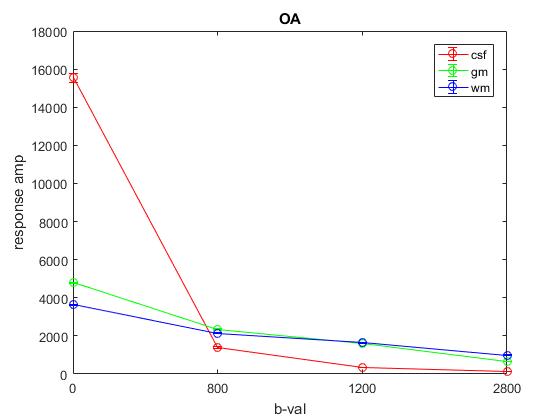
Plot of average response (1st column) across OA:
Plot of average response (1st column) across All:
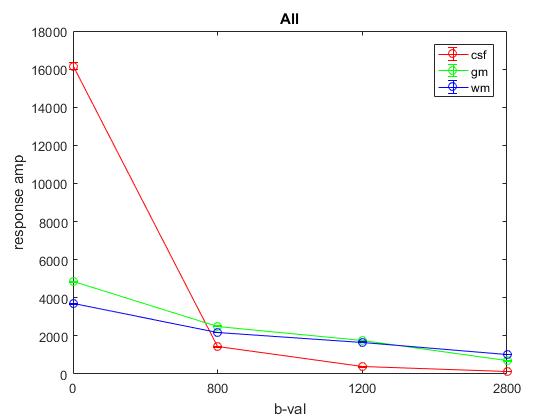
Plot of responses normalized to CSF(1,1) averaged across YA:
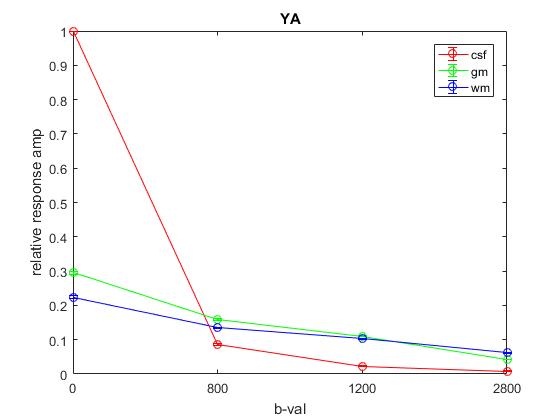
Plot of responses normalized to CSF(1,1) averaged across OA:
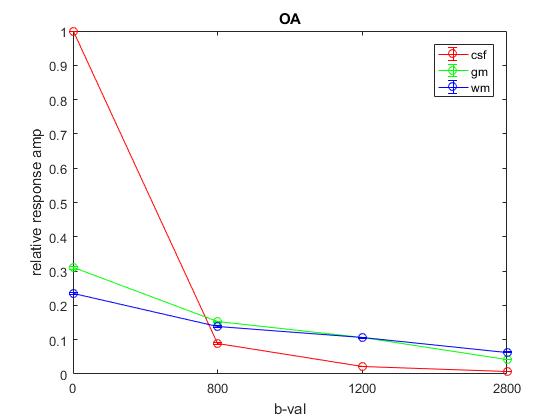
Plot of responses normalized to CSF(1,1) averaged across All:
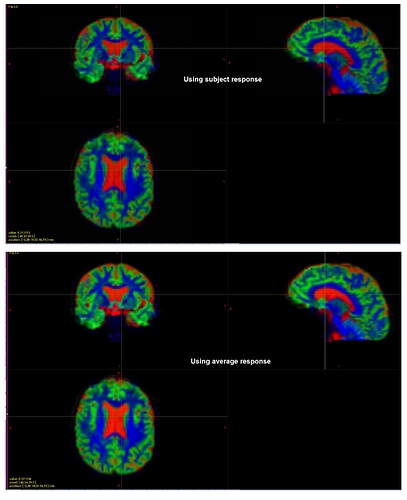
TissueRGB for the exemplar old adult using subject and average (across all) response:
Do you think they look fine?
Please let me know if you need more info/outcome.
Cheers,
Hamed
Hi @Hamed,
These results look very good! It’s good to see that the average responses across YA are very similar to those across OA; this adds confidence that the algorithm robustly extracts the responses of the specific tissue types it’s after! A small tip if you want to show such a response function plot as part of a presentation or publication: make sure the b-values on the horizontal axis aren’t just labels at fixed interval distances, but actually put them where they belong on the b-value axis (e.g. if using matlab for this purpose, create a vector [0 800 1200 2800] and plot the amplitudes in function of this vector). This further helps appreciate the “shape” or the decay of each response, and how these shapes relate to each other across the tissue types.
Your MSMT-CSD results also look good; very much the expected quality. If your intention is to do quantitative analysis of any sort (e.g. fixel-based analysis of FD), it’s important to use the (same) average response function for all subjects in all groups. The response functions can be seen as the units of your tissue maps (and as such, the unit of the FD metric from the FOD), and when you compare stuff quantitatively, of course you want to use the same units across the board!
Cheers,
Thijs
Hi Thijs
Thanks for the confirmation. Of course I could (and probably will) not accomplish dwi analysis without the help of Mrtrix experts. 
Regarding plotting, you are absolutely right. It was done very fast.
Regarding responses, I did some stats on the raw (and not normalized) values and although the pattern is similar for both Age groups but there are slight (and significant) differences between them. I think this is also expected and is the reason why one should use the (same) average response across groups.
Here are the stats:
For all tissue types there is a significant main effect of Age (YA>OA) and Age x b-val interaction is significant for GM & CSF tissue responses.
Cheers,
Hamed
Interesting finding, and spot on: if you were to not use the same responses across groups, these effects would disappear from the (FOD) results. It’s, in a way, quite simple really: either such effects sit in the responses, or in the ODFs, or they’re spread out between both. That’s why, for e.g. fixel-based analysis one should use the same responses; otherwise the interpretation becomes exceptionally tricky (and potentially non-specific).
Just using the (dhollander) response function algorithm and averaging the responses for each group separately, and then looking at the differences between those (as in your post) is an interesting approach in a way as well. You’re avoiding doing registration, as the “registration” is essentially done by the response function estimation algorithm then, which finds “matching” (not spatially per se, but in other properties) single-fibre WM, GM and CSF regions for you, and extracts the main properties of the signal (the response functions) in those regions for you. Always proceed with care though, as there are many nuances to interpreting such a result, some of which may depend on the cohorts you’re dealing with. But I happily encourage exploring uses for the response function(s) obtained from the algorithm… there’s lots of interesting opportunities. 
