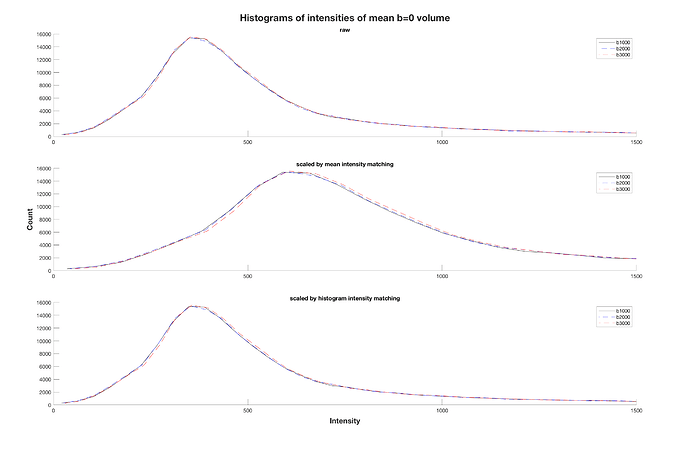
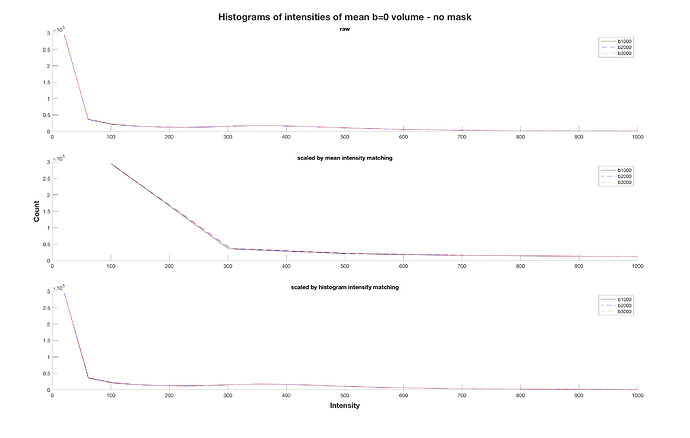
I also came across mrhistmatch scale after I posted my question, using the b=0 from the b2000 and b3000 acquisitions as input images and the b=0 from b1000 as target. I used the same brain mask as mask_input and mask_target, simply obtained with dwi2mask on the b1000 acquisition. However, the mean b=0 intensity of the scaled images was not equal across series. From what you mention, I can assume that this is due to an improper use of the brain mask?
Well, if dwicat were to not use mrhistmatch scale, and instead just set the mean b=0 intensity (optionally within a mask) to some fixed value, then one would expect that following dwicat, the mean b=0 intensity (within the mask if a mask was used) would be that fixed value and hence identical across series. So assuming that you either used a mask for both intensity matching and testing of the intensity matching, or you didn’t use a mask in either case, the masking is a red herring.
The reason why the mean b=0 intensities don’t match exactly in this case is because that’s not what mrhistmatch scale does. If it just took the mean intensities and made them equivalent, I’m not sure if that would classify as “histogram matching”; “intensity matching” maybe.
Now here’s where things get weird (and this is possibly another source of internal doubt about more widely advocating the use of dwicat). And hopefully I get this right and don’t make a fool of myself.
What’s actually happening is that the image intensities are all being sorted and concatenated into a large linear equation, the solution to which is the scaling factor that makes those histograms most similar to one another. If using mrhistmatch linear, this linear system formulation is necessary in order to simultaneously estimate both a slope and intercept for modulating the intensities of one image to match another. But in the case of mrhistmatch scale, this linear system of Ax=b has A as a N x 1 vector of input image intensities, x is a 1 x 1 “matrix” which is just the scaling factor, and b is a N x 1 vector of target image intensities (there’s some internal trickery in here to deal with the case where the target image may not have the same number of voxels as the input image, but I’ll spare the headache as much as possible).
This gets solved using the Normal Equation (as of 3.0.2):
ATAx = ATb
Both ATA and ATb are just scalars. So really, what mrhistmatch scale is doing is finding the right multiplicative factor:
x = ATb / ATA
that will make (input_image x target_image) equivalent to (input_image x input_image), where this is a kind of multiplication of “corresponding” intensities between two images.
This contrasts against just making the mean b=0 image intensities equivalent, which in this notation (and limited typesetting) would look something like:
x = mean(b) / mean(A)
So the fact that mrhistmatch scale is doing something different to just making the means equivalent means ( ) that the means won’t necessarily be equivalent afterwards. Your homework question is: Is the former approach better?
) that the means won’t necessarily be equivalent afterwards. Your homework question is: Is the former approach better? 
does dwicat also rely on the use of a good brain mask to achieve a good result (if it is basically doing the same as mrhistmatch)?
I’d say that the precision of dwicat is better if it can be provided with a reasonable mask. It works without one, but the fact that you then have a lot of pure-noise voxels contributing to the intensity matching means that the estimates are not quite as good. I did some testing at the time where I extracted different b=0 volumes, artificially scaled them, and then checked the scaling factors estimated within dwicat, and from memory the errors relative to the actual induced scaling were less if a mask was used. But this was not robust testing across a range of datasets.
Since this might not be trivial, then I think I would be better off maybe scaling the mean intensity “by hand” (with the above mentioned approach), and then concatenate them with mrcat instead, no?
Better would be to modify dwicat to have a command-line option to use the mean b=0 intensity of each series for determining the appropriate scaling factors instead of mrhistmatch. That would take far less effort overall if you have a lot of data to process. But I would not expect use of the mean intensity to be any less dependent on masking than the mrhistmatch approach.
Would then this be a non-fundamental issue in my case?
If it’s purely single-subject analysis, then it’s likely the case that the whole pipeline is in fact invariant to this process. However if you’re doing a group analysis, and hence using group-averaged response functions, then fluctuations of image intensities within specific shells would bias the tissue decomposition in one direction or another.
Regardless of the specific method, is there a specific order how they should be concatenated? (e.g. all b0s stacked at the beginning of each shell?)
Not for any MRtrix3 commands. Anything that is b-value dependent will explicitly group image volumes into “shells”, and interpret them based on the diffusion sensitisation direction (or equivalently to one another in the case of b=0 volumes), and so is order-independent both within and between shells.
Rob
 greatly appreciated!
greatly appreciated!