Welcome Pietro!
Always love an introduction that starts with my methods producing unexpected results!  (jk)
(jk)
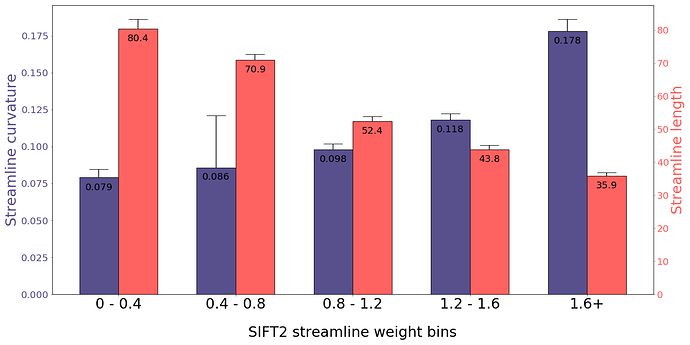
I’ll start with length, since explaining the curvature probably depends on understanding the length effect.
While I don’t think I’ve demonstrated anything in this regard specifically with SIFT2, you could infer that this is the result that you would get based on Figure 7 in this manuscript. There, I show that SIFT tends to retain short streamlines and remove long streamlines. SIFT2 is simply a more continuous version of that effect.
(Indeed one way of conceptualising SIFT is that it assigns a weight of 0 to “removed” streamlines, and some fixed weight > 1.0 to all “retained” streamlines)
The deep white matter pathways, where the FODs are less complex and there is no partial volume with grey matter, and a large volume in which to seed in the case of homogeneous streamline seeding, tends to make those deeper long-range connections “easier” to track, and therefore over-represented in an unfiltered tractogram. The short-range superficial pathways near the cortex often result in streamline reconstruction failure (even with ACT’s back-tracking), and so end up under-represented in the unfiltered tractogram. SIFT2 is compensating for that effect as I would expect it would. In fact as I type this I’m wondering if 3.0.0's reduction of the default FOD amplitude threshold during tractography might reduce this effect, as there should be less premature streamline terminations in the superficial white matter…
The story for curvature is a little more complicated. There’s potentially a few things going on there.
For a definitive answer, you would need to include the details of precisely how mean curvature is being calculated:
-
If you were to calculate curvature purely on a vertex-by-vertex basis, i.e. with no smoothing, then I would expect a mild correlation between curvature and streamline length. This would be driven purely by the fact that in deep WM, the FODs tend to be less complex, with less dispersion within each lobe, and so streamlines will tend to “wobble” a bit less when tracking along a major bundle, and less frequently take sharp turns to leap from one lobe to another.
-
For short streamlines, the two endpoint vertices are a greater fraction of the total streamline vertex count than they are for longer streamlines. Depending on precisely how this is handled, a small bias may be introduced between calculation of curvature between short v.s. long streamlines.
-
If you are calculating curvature in a manner that incorporates smoothing (e.g. this code not directly accessible, but utilised by tckmap -contrast curvature), then the effect of discontinuity at the streamline endpoints may have a greater effect.
In general though, I don’t see any particular reason why streamline curvature would have a direct influence on SIFT2 weights, given how the relevant calculations are done. I suspect more likely what’s going on is:
-
SIFT2 tends to upweight short streamlines and downweight long streamlines;
-
Long streamlines have less curvature than short streamlines.
I.e. It’s an indirect correlation.
I reckon if you were to use the vectorstats command to test the hypothesis of a non-zero correlation between SIFT2 weight and streamline curvature, but removed the effect of streamline length using the Freedman-Lane method, the null hypothesis would not be rejected. 
Cheers
Rob
 (jk)
(jk)