TODI / FOD registration and normalisation

[fionaEyoung]

Hello community!

I’m working on an analysis of an individual tract in the brain using track orientation density imaging (TODI). I have tractograms (or.tck) for 20 subjects. In brief, I’m having trouble with

1. transforming FODs into an MNI template (am I missing a key point about effectively transforming FODs?)
   AND
2. normalising FODs (am I going about this correctly?)

(I can achieve 1. and 2. individually, but not combined)

The aim is to have an average, normalised orientation distribution map of the tract in an MNI template space (I’m using MNI152, originally 1mm voxels, downsampled to 2.5mm to match subject diffusion).
By normalised I mean an orientation distribution function in each voxel that integrates to 1.

I’m using the track orientation density image (TOD) obtained by

tckmap -tod 8 OR_tractogram.tck tod.mif

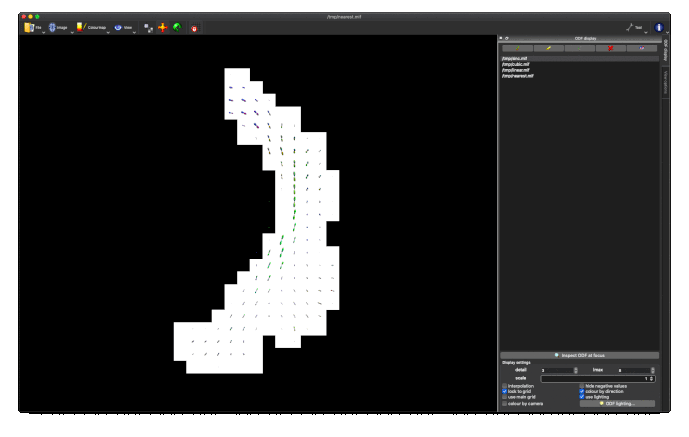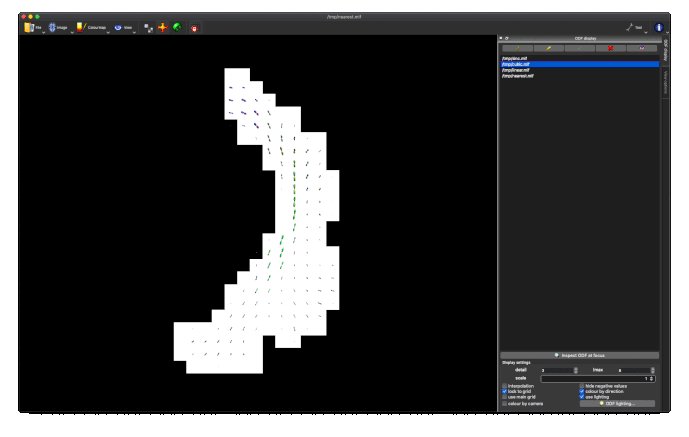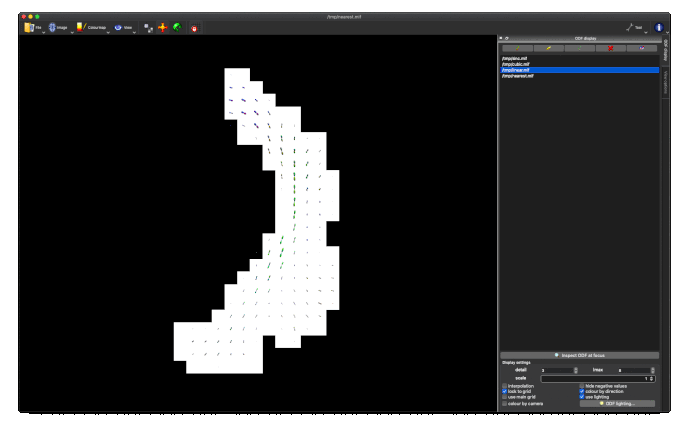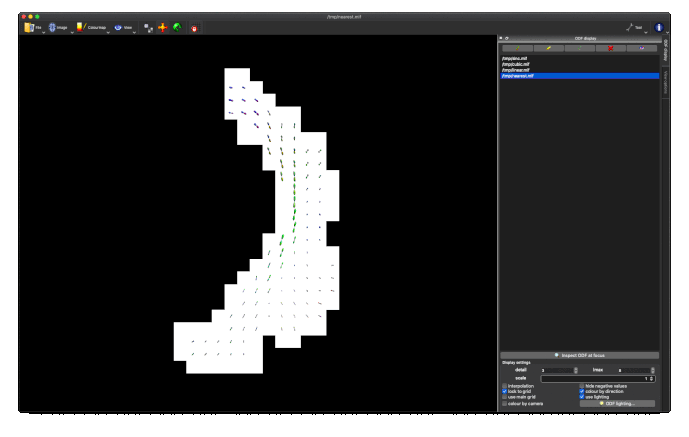
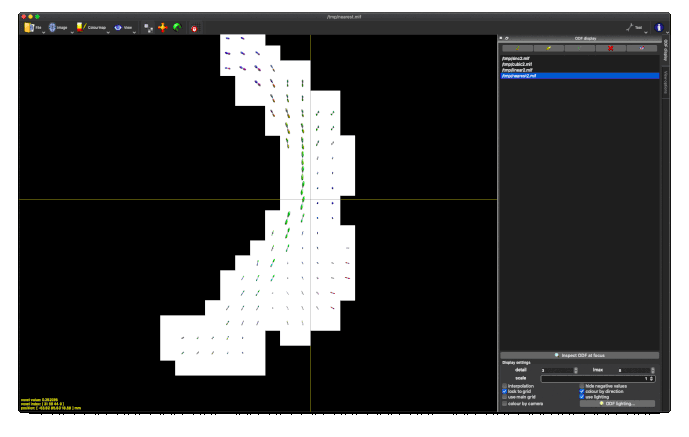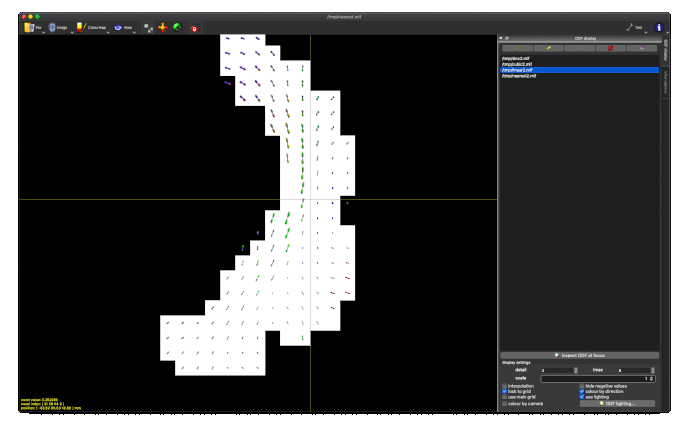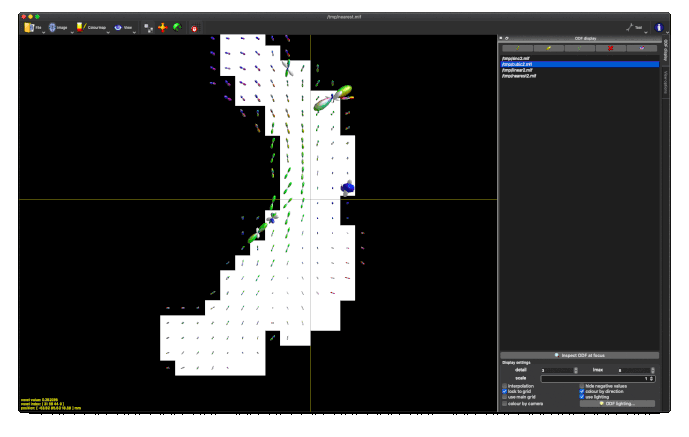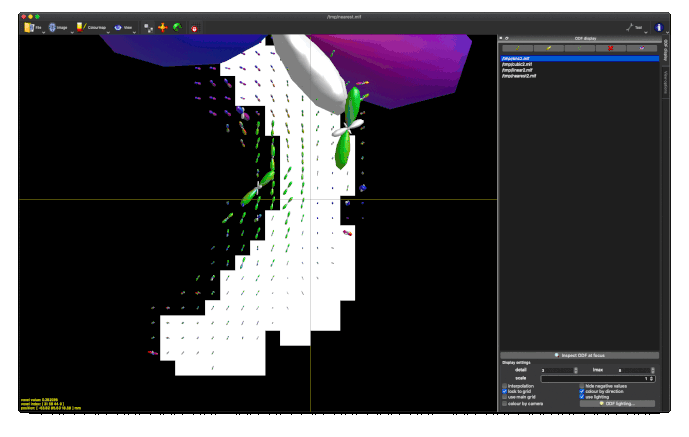
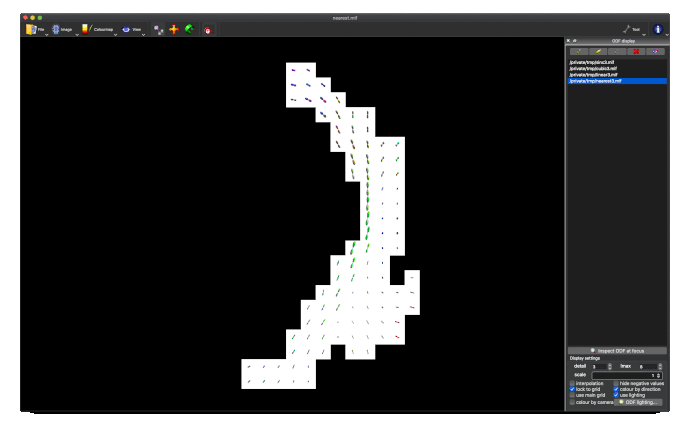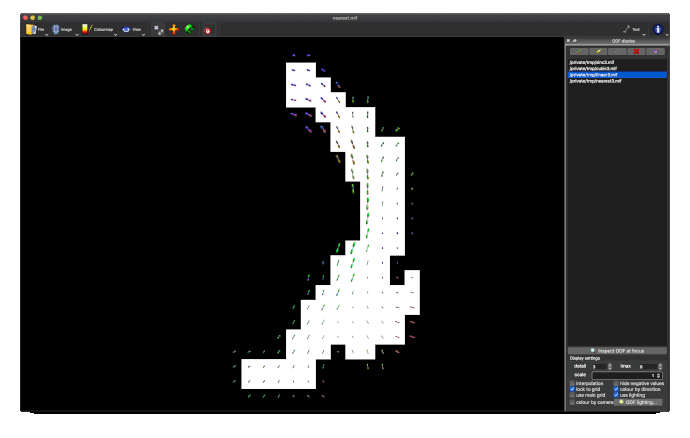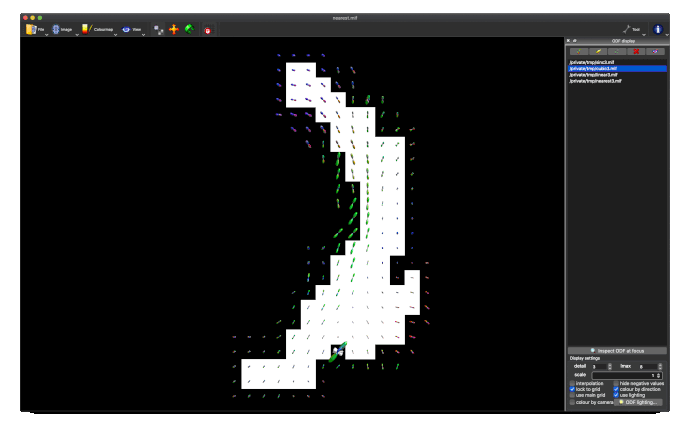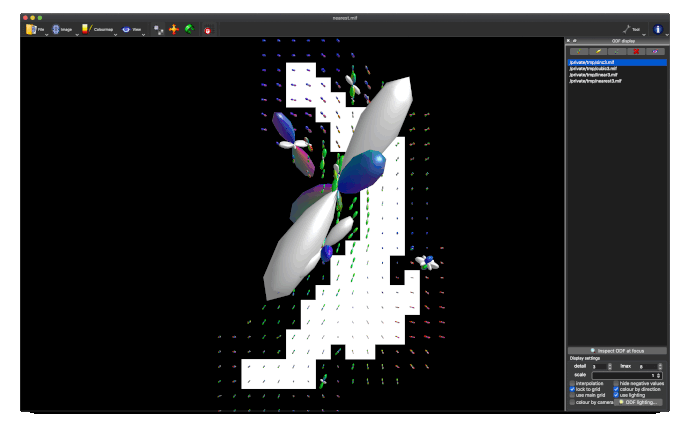
The output tod.mif (above, right) contains the (scalar) track density information which I want to normalise out, to obtain a pdf.
My understanding is that this effectively equates to dividing the full TOD by the first TOD spherical harmonic coefficient and sqrt(4pi):

mrconvert -axis 3 0 tod.mif tod0.mif
mrcalc tod.mif tod0.mif 4 pi -mult -sqrt -mult -div todnorm.mif

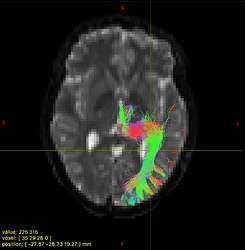
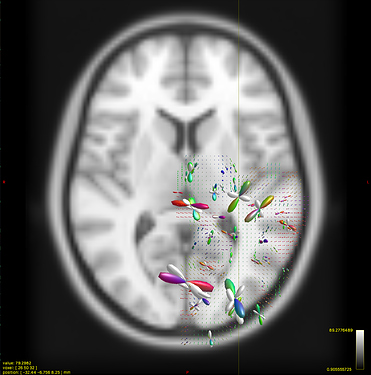
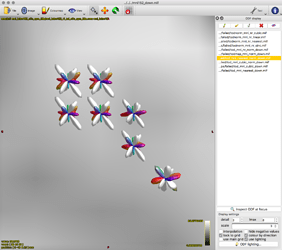
This works really nicely in subject diffusion space:

I’m having less success when adding registration into the mix.

Each subject has a T1 image which has already been aligned with subject diffusion space.
Using fsl’s FLIRT, I’ve registered each subject T1 to the MNI template (affine, 12 dof),
converted the transformation to mr format, and transformed the subject TOD images.

mrtransform -linear t_t1_2_mni_mr.txt -template mni152_down.mif tod.mif tod_mni.mif

I can’t seem to achieve a well behaved, normalised TOD map in MNI space.
I’ve tried (put simply):

1. normalising in subject space, then transforming
2. transforming, then normalising in template space

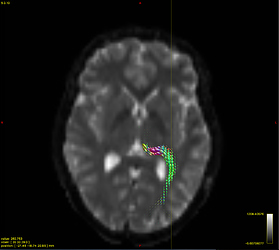
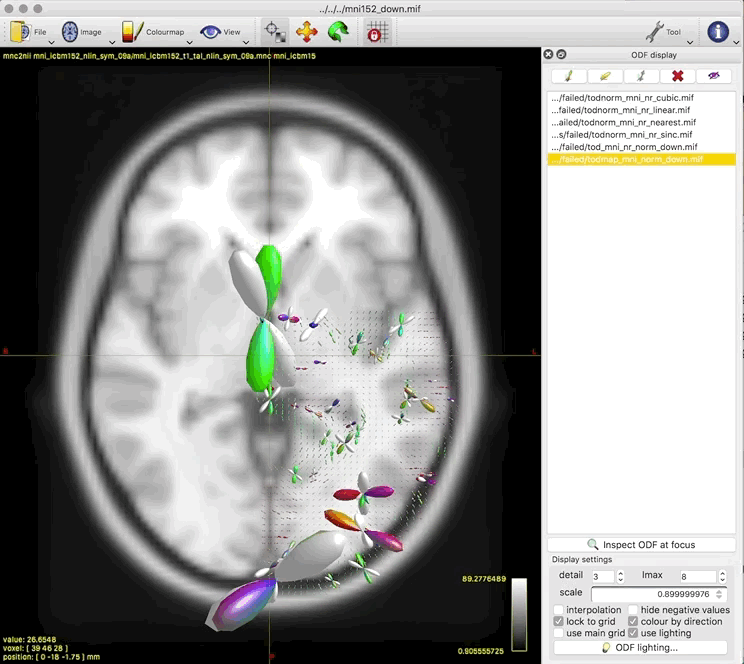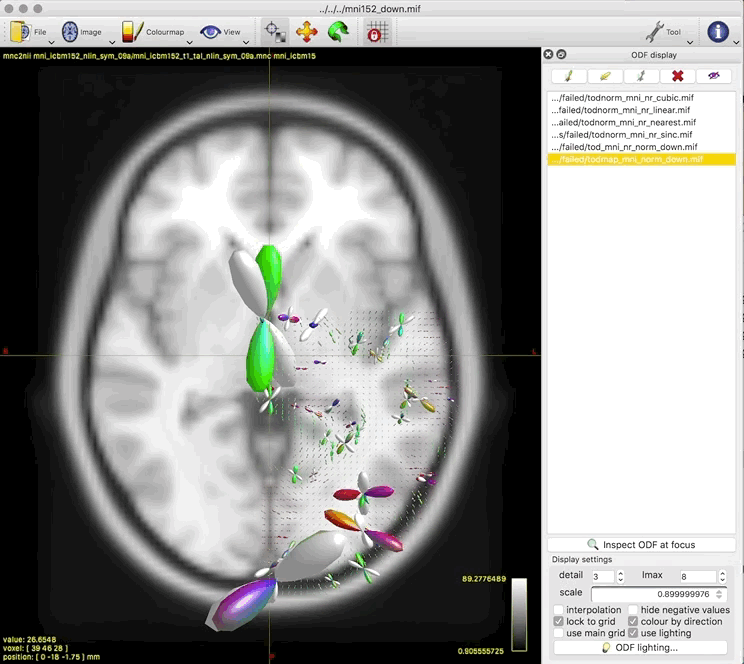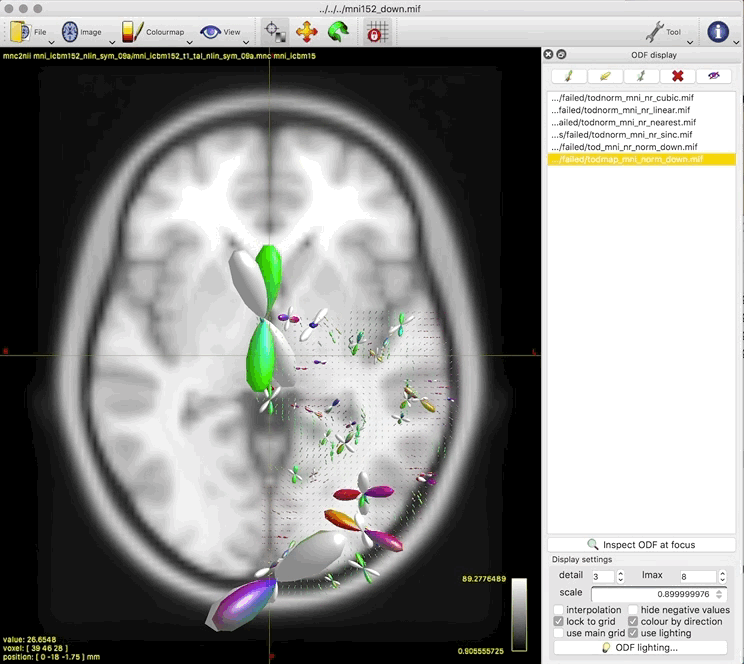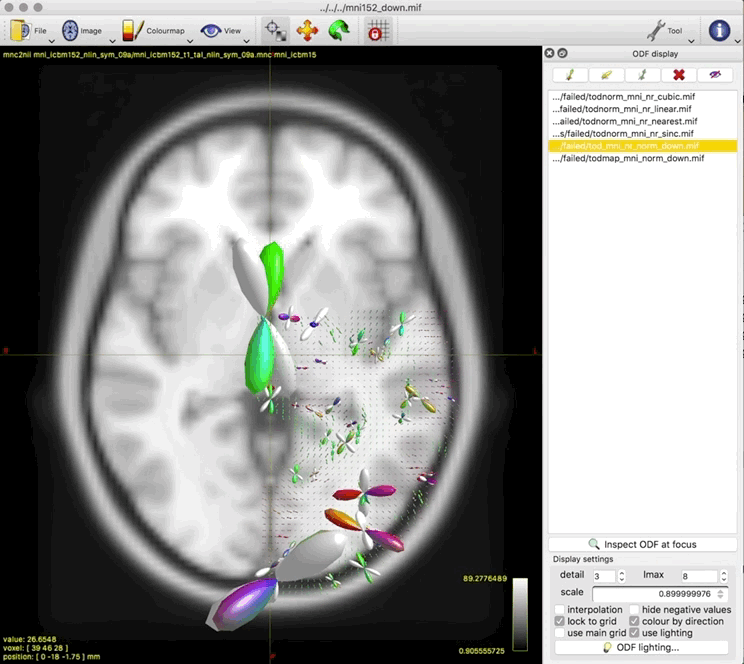
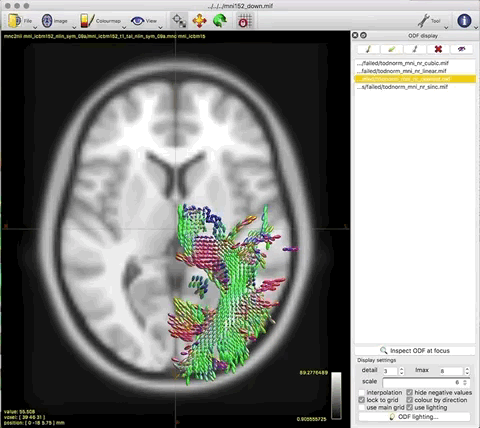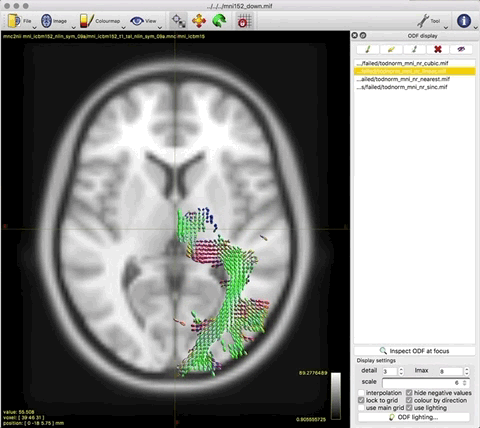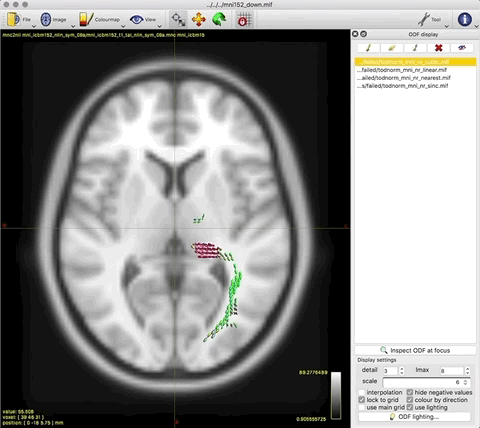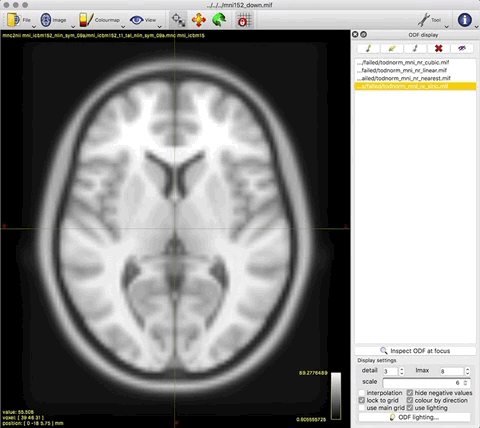
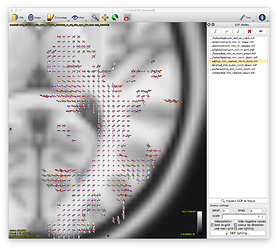
Option 1. results in a large reduction in the apparent extent of the tract,
as if lots of the tract ODFs at the edge have been suppressed to zero:

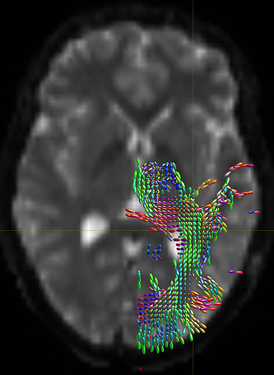
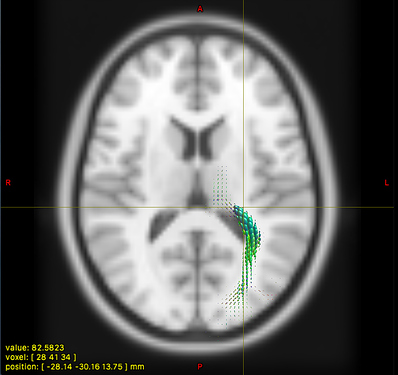
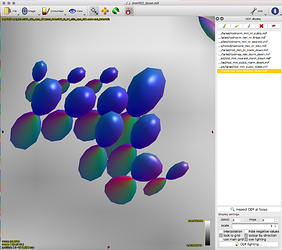
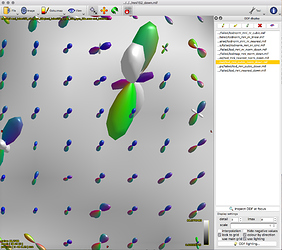
Option 2. results in a (seemingly random, although typically located in low track density regions) selection of ODFs blowing up and gaining negative lobes:

Things that look fine:

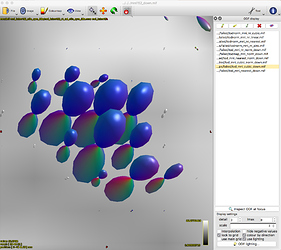
• normalised TOD in subject space (above, 3rd image)
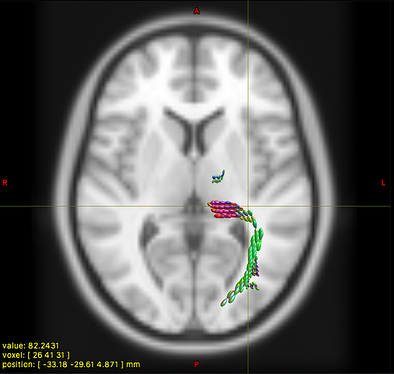
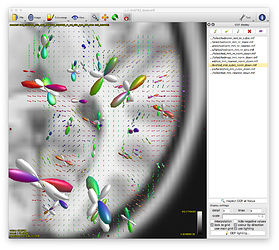
• unnormalised TOD transformed to MNI:

I have only a limited understanding of SH ODFs, and particularly the reorientation process using apodised PSFs, but I had a suspicion that small numbers and rounding errors might be the culprit. However, first scaling the TOD map by 200 before transforming and normalising made no noticeable difference, so now I’m really at sea. I’ve also attempted creating the TOD map at higher angular resolution (up to lmax 14) to no avail. Any tips / experiences appreciated!

MRtrix version: 3.0_rc3
OS: Mac OS X 10.13.6

Cheers,
Fiona

Side question: What does the “interpolation” option in the mrview ODF display tool do? When I uncheck it, a whole bunch of extra ODFs appear at the edges of the tract, and the rest are unchanged. All of the above images have this ODF interpolation turned off.

[Apologies for the long post, I tried to keep it to the point while including enough useful details]

[fionaEyoung]

Update! I think I’ve solved the problem! (typical, you bash your head against something for weeks and as soon as you ask for help you figure it out… )

Both methods mentioned above (normalise then transform, or transform then normalise)
now work and give the same results when nearest interpolation is used when transforming the TOD images (mrtransform -interp nearest ...).

I suppose this ties in with my side question about ODF interpolation. I’m surprised that the choice of interpolation method would have that drastic an effect (in particular the amount of “erasure” occurring when transforming the normalised FODs).

[maxpietsch]

Hi Fiona,

A few things to unpack here. With your normalisation, you remove all density information and only retain angular information. Voxels with minuscule densities (noise) appear as large as ODFs inside the OR. I have a hard time thinking about use cases for such data but let’s assume this is what you want to do.

If I understand correctly, I think the effects you are seeing are likely due to numerical issues related to the way you perform the normalisation, let’s also rule out possible mistakes in the processing.

@fionaEyoung

normalising in subject space, then transforming … results in a large reduction in the apparent extent of the tract, as if lots of the tract ODFs at the edge have been suppressed to zero:

This doesn’t look right. Are you sure you used the normalised image? This looks more like a tod.mif image transformed.

@fionaEyoung

transforming, then normalising in template space … results in a (seemingly random, although typically located in low track density regions) selection of ODFs blowing up and gaining negative lobes:

Did you use the first volume of the transformed TOD image to normalise this image?

mrtransform -linear t_t1_2_mni_mr.txt -template mni152_down.mif tod.mif tod_mni.mif
mrconvert -axis 3 0 tod_mni.mif - | mrcalc tod_mni.mif - 4 pi -mult -sqrt -mult -div todnorm_mni.mif

@fionaEyoung

I have only a limited understanding of SH ODFs, and particularly the reorientation process using apodised PSFs, but I had a suspicion that small numbers and rounding errors might be the culprit. However, first scaling the TOD map by 200 before transforming and normalising made no noticeable difference, so now I’m really at sea. I’ve also attempted creating the TOD map at higher angular resolution (up to lmax 14) to no avail. Any tips / experiences appreciated!

ODF reorientation is not a lossless operation and can introduce errors. You can transform the images without reorientation to verify its effect on the amplitude of the data. The occurrence of negative lobes can be reduced by increasing the number of directions (dirgen, mrtransform -directions) but I don’t think this is the major issue here.

@fionaEyoung

What does the “interpolation” option in the mrview ODF display tool do? When I uncheck it, a whole bunch of extra ODFs appear at the edges of the tract, and the rest are unchanged. All of the above images have this ODF interpolation turned off.

If checked, mrview uses linear interpolation of the ODF coefficients, otherwise nearest interpolation. If the main image grid does not match that of the ODF image or if the image is viewed not snapped to an axis location, you’d probably want to interpolate ODF values.

@fionaEyoung

Both methods mentioned above (normalise then transform, or transform then normalise)
now work and give the same results when nearest interpolation is used when transforming the TOD images ( mrtransform -interp nearest ... ).

Not sure I understand what’s going on there. Non-nearest interpolation causes small values at the edge of the tract. If there are numerical issues then this could amplify these. Your voxel-wise normalisation after transformation makes voxels that contained arbitrarily little ODF (due to partial volume effects with non-tract areas) look like any other voxel so in effect you are amplifying the noise in these areas. That doesn’t necessarily mean nearest neighbour interpolation is the right thing to do (for illustration, use it on an image), I’d argue your normalisation is questionable. I think the “erasure occurring when transforming the normalised FODs" is not caused by the transformation. Can you please double-check the command history of the file (mrinfo -property command_history) and verify if the input to mrtransform is actually normalised? If so, feel free to share the input, output and mni template images and transformation file with me so we can check what is going on.

Cheers,
Max

[fionaEyoung]

Hi Max

Thanks for taking a look at this.

@maxpietsch

This doesn’t look right. Are you sure you used the normalised image? This looks more like a tod.mif image transformed.

It’s reassuring that you share my incredulity on this. For comparison, the last image in my original post is the transformed tod.mif image, where the density scaling is clearly visible.

@maxpietsch

Can you please double-check the command history of the file ( mrinfo -property command_history ) and verify if the input to mrtransform is actually normalised?

$ mrinfo -property command_history todmap_norm_mni_down.mif            
mrcalc "rois_and_tracks/todmap.mif" "rois_and_tracks/tdi.nii" "-div" "todmap_norm.mif"  (version=3.0_RC3-137-g5d6b3a6f)
mrtransform "-linear" "mnireg/t_t1_2_mni152_mr.txt" "-template" "../mni152_down.mif" "maps/todmap_norm.mif" "maps/todmap_norm_mni_down.mif"  (version=3.0_RC3-137-g5d6b3a6f)

@maxpietsch

Did you use the first volume of the transformed TOD image to normalise this image?

Yep!

$ mrinfo -property command_history  todmap_mni_norm_down.mif
mrtransform "-linear" "mnireg/t_t1_2_mni152_mr.txt" "-template" "../mni152_down.mif" "maps/todmap.mif" "maps/todmap_mni_down.mif"  (version=3.0_RC3-137-g5d6b3a6f)
mrcalc "-force" "todmap_mni_down.mif" "tod0map_mni_down.mif" "4" "3.14159265359" "-mult" "-sqrt" "-mult" "-div" "todmap_mni_norm_down.mif"  (version=3.0_RC3-137-g5d6b3a6f)
$ mrinfo -property command_history tod0map_mni_down.mif
mrtransform "-linear" "mnireg/t_t1_2_mni152_mr.txt" "-template" "../mni152_down.mif" "maps/todmap.mif" "maps/todmap_mni_down.mif"  (version=3.0_RC3-137-g5d6b3a6f)
mrconvert "-coord" "3" "0" "todmap_mni_down.mif" "tod0map_mni_down.mif"  (version=3.0_RC3-137-g5d6b3a6f)

@maxpietsch

ODF reorientation is not a lossless operation and can introduce errors. You can transform the images without reorientation to verify its effect on the amplitude of the data.

This is an interesting point. I checked transformation with and without reorientation (followed by normalisation in MNI space) and saw no effect on the occurrence of negative lobes:

@maxpietsch

Not sure I understand what’s going on there.

@maxpietsch

That doesn’t necessarily mean nearest neighbour interpolation is the right thing to do (for illustration, use it on an image),

@maxpietsch

I think the “erasure occurring when transforming the normalised FODs" is not caused by the transformation.

Not by the transformation, but by the interpolation method, and while I can’t provide a rigorous mathematical explanation, it makes qualitative sense to me that interpolation could be (part of) the issue. There are 4 different possible interpolation methods, the default being cubic. The key difference between them is the size of neighbourhood used to compute the new value, and a voxel at the very edge of the tract with an ODF may only have one or two neighbours that are non-zero. Also, unlike “normal” image values, SH coefficients can be negative, so interpolated values could conceivably be (effectively) zero.

To illustrate, I ran transformation of the normalised TOD image, without reorientation, for each different type of interpolation:

mrtransform -linear mnireg/t_t1_2_mni152_mr.txt -template mni152_down.mif  -noreorientation todmap_norm.mif todnorm_mni_nr_linear.mif -interp linear

etc.

Here are the results, ordered by increasing size of neighbourhood used: nearest (lots of ODFs), linear, cubic, sinc (empty)

For the very last image using sinc interpolation, I checked using mrstats and indeed, every coefficient is zero everywhere!

It seems that this effect only applies when transforming (and interpolating) normalised ODFs (each with the same density, or first coefficient). Things get weird when transforming the tod.mif image.

mrtransform -linear mnireg/t_t1_2_mni152_mr.txt -template mni152_down.mif  tod.mif tod_mni_nearest_down.mif -interp nearest

Here is a comparison of transformation without any normalisation applied, with nearest (left) and cubic (right) interpolation:

And here are the same two images, after normalisation

mrconvert -coord 3 0 tod_mni_nearest_down.mif - | mrcalc tod_mni_nearest_down.mif - 4 3.141592654 -mult -sqrt -mult -div tod_mni_nearest_norm_down.mif -force

Same again, full picture:

@maxpietsch

I’d argue your normalisation is questionable.

Perhaps. It seems to me that there is something funky going on with the combination of transformation, interpolation and normalisation, as the above image pairs were produced in identical manner save for the mrtransform -interp option.

Anyhow, it may be that this interests nobody except me, and it indeed comes down to some minute numerical error or noise effect. I’ll continue investigating the “normalise, then transform” option, without interpolation, as it seems to be the most well behaved option. I’ve compared the ODF shapes up-close between the different interp methods and the difference is negligible for my purposes. If you’re still perplexed / curious I can look into sharing the files with you!

Cheers
Fiona

(Apologies for the liberal use of animated gifs, I know some people detest them but I think its the best way of seeing small differences!)

[ThijsDhollander]

Hi Fiona,

Ok, there’s a million things going on here. But, to make sure I get it right (so do correct me if I don’t!), we’re essentially talking about 3 main operations here:

1. Computing the TOD from a set of streamlines (i.e. tckmap)
2. Normalising the TOD so it becomes an ODF that integrates to 1 (or a constant at least; so getting rid of the total magnitude, retaining only the angular distribution)
3. Transforming to MNI space via a linear transformation; which then also involves a choice of interpolation

I noticed you use a separate TDI image at times in the normalisation. In principle this should be correct, but if it doesn’t match the TOD image exactly in how it was generated, interpolated, … or taken through any other steps, you’ve got a problem. It’s safer here to use the command Max mentioned:

mrconvert -axis 3 0 tod_mni.mif - | mrcalc tod_mni.mif - 4 pi -mult -sqrt -mult -div todnorm_mni.mif

The 4 pi -mult -sqrt -mult bit in there isn’t per se crucial depending on what you intend to do; but in any case, that’s essentially a constant. For the sake of intuition, if you ignore that for a moment, what the command does before the pipe (the mrconvert bit) is so first extract the first volume of the TOD image: the key thing to understand here is that this volume is a TDI image ; it’s the magnitude part of the TOD. The nice thing is that it goes exactly with it, so no need to juggle around a separate TDI image. That might already avoid a range of potential weird things that could otherwise happen.

However, you might not want to even warp / transform the TOD image per se: whatever interpolation you use, you’re unnecessarily going to lose some precision at that step. So to avoid any an all issues all together, think about switching around the order of the whole pipeline like this:

1. Warp / transform to MNI space, then…
2. Compute TOD, then…
3. Normalise using the above command

This will be a (just very slightly though) more precise end result, but it’ll also avoid warping (and interpolating) the TOD. Your options for step 1 in this new order of things include:

• Warping / transforming the streamlines.
• Or if you don’t want to deal with that, and assuming your .tck came from tractography on FODs e.g. via tckgen (?), then instead warp / transform the original FOD image before tractography, and perform your tractography itself on the transformed FOD image in MNI space. I won’t go into all the details here, but depending on what you’re after in the end, this might be the least biased way to go about the entire thing as well.

See if you can give one of these latter 2 options a go; and you’ll avoid a few particular risks as to imprecisions. The TOD will also more fairly represent the track distribution within the actual voxels of your MNI template space; and thus be the closest to representing the same kind of thing across your 20 subjects (i.e. less confounds if you intend to compare or combine or … these across the 20 subjects).

Cheers & take care,
Thijs

[maxpietsch]

@fionaEyoung

If you’re still perplexed / curious I can look into sharing the files with you!

I am. Does your original TOD map contain NaNs? Feel free to send me the files
mnireg/t_t1_2_mni152_mr.txt mni152_down.mif todmap_norm.mif maps/todmap.mif and the original TOD map (I think one of `maps/todmap.mif, rois_and_tracks/todmap.mif). The interpolation gif shows that something odd is going on.

@fionaEyoung

Not by the transformation, but by the interpolation method

In any case, I’d second what Thijs suggested, warp the .tck file (using the inverse transformation, see here) to template space and generate the images there should, from what you describe, solve the normalisation issue. This doesn’t solve the open questions, so if you can share the data, I’d be happy to investigate.

[fionaEyoung]

Hi Thijs

Thank you for your input, and it’s true, there are so many things going on at once!

@ThijsDhollander

to make sure I get it right

you have absolutely got it right

@ThijsDhollander

The nice thing is that it goes exactly with it, so no need to juggle around a separate TDI image.

This is a good point. I think the very first rookie normalisation I did was using a separate TDI image, after that I switched to normalising with TOD volume 0, as you suggest.

@ThijsDhollander

So to avoid any an all issues all together, think about switching around the order of the whole pipeline like this

@maxpietsch

I’d second what Thijs suggested, warp the .tck file (using the inverse transformation, see here)

This is a good workaround. For some reason I was reluctant to transform the streamlines on account of tcktransform only accepting a warp image instead of a transformation matrix, but I bit the bullet and the results look good.
Incidentally, the results look visually very similar to the “normalisation-then-transformation-with-nearest-interpolation” results. But that’s not necessarily an indication of what’s going on under the bonnet and I agree that this is a sounder pipeline.

[fionaEyoung]

@maxpietsch

Does your original TOD map contain NaNs?

That hadn’t occured to me, but it would appear not (if my command is sound)

$ mrcalc todmap.mif -isnan - | mrstats - -allvolumes
mrcalc: [100%] computing: isnan (todmap.mif)
      volume       mean     median      stdev        min        max      count
      [ 45 ]          0          0          0          0          0   24883200

[maxpietsch]

I think NaNs are one issue, interpolation in conjunction with voxel-wise division is another:

1. normalise, then transform

transformed images are not normalised due to non-nearest interpolation

nansanitise=true
for interp in nearest linear cubic sinc; do
	echo $interp
	a=$(mrconvert ODF.mif -coord 3 0 - | mrcalc ODF.mif - 4 3.14159265359 -mult -sqrt -mult -div -)
	if $nansanitise; then 
		a=$(mrcalc $a -isnan 0 $a -if -)
	fi
	mrtransform  -linear R.txt $a -reorient yes -interp ${interp} ${interp}.mif -template mni_t.mif -force
done

If you want normalised data after transformation, nearest interpolation is probably the best choice, however interpolation is also required for the angular domain. The other interpolation options would need to be normalised again, amplifying partial volume effects (problematic in particular as you already have voxel-wise scaled your data).

2. transform then normalise

noise amplified due to normalisation in partial volume areas

for interp in nearest linear cubic sinc; do
	mrtransform -linear R.txt ODF.mif -reorient yes -interp ${interp} -template mni_t.mif a.mif -force
	a=$(mrconvert a.mif -coord 3 0 - | mrcalc a.mif - 4 3.14159265359 -mult -sqrt -mult -div - -force)
	if $nansanitise; then 
		mrcalc $a -isnan 0 $a -if ${interp}2.mif  -force
	else
		mrcalc $a ${interp}2.mif -force
	fi
done

for interp in nearest linear cubic sinc; do
	echo $interp
	mrconvert ${interp}.mif -coord 3 0 - -quiet | mrstats -
	mrconvert ${interp}2.mif -coord 3 0 - -quiet | mrstats -
done

nearest
      volume       mean     median        std        min        max      count
       [ 0 ] 6.18801e-05          0 0.00417759          0   0.282095     902629
      volume       mean     median        std        min        max      count
       [ 0 ] 6.18801e-05          0 0.00417759          0   0.282095     902629
linear
      volume       mean     median        std        min        max      count
       [ 0 ] 5.91631e-05          0 0.00342176          0   0.282095     902629
      volume       mean     median        std        min        max      count
       [ 0 ] 0.000136886          0 0.00621258          0   0.282095     902629
cubic
      volume       mean     median        std        min        max      count
       [ 0 ] 5.82268e-05          0  0.0035755 -0.0149693   0.306932     902629
      volume       mean     median        std        min        max      count
       [ 0 ] 0.000224706          0 0.00795852          0   0.282095     902629
sinc
      volume       mean     median        std        min        max      count
       [ 0 ] 5.8517e-05          0 0.00360018 -0.0247972   0.313869     902629
      volume       mean     median        std        min        max      count
       [ 0 ] 0.00039597          0  0.0105615          0   0.282095     902629

3. renormalise 1.

for interp in nearest linear cubic sinc; do
	mrconvert ${interp}.mif -coord 3 0 - | mrcalc ${interp}.mif - 4 3.14159265359 -mult -sqrt -mult -div ${interp}3.mif -force
done

heavy corruption by interpolation and scaling artefacts:

[rsmith]

For clarity:

mrcalc tod.mif tod0.mif 4 pi -mult -sqrt -mult -div todnorm.mif

Option 1. results in a large reduction in the apparent extent of the tract,

For voxels where the value of tod0.mif is 0 (i.e. no intersecting streamlines), the value in image todnorm.mif will be NaN due to division by zero.
Then, when you perform a non-linear transformation of those data, any voxel in the template image space for which any voxel in a 4x4x4 neighbourhood around the input image sampling point is NaN (due to use of cubic interpolation), the TOD image in template space will also be NaN.
This is why the bundle becomes thinner as a result of transformation: the NaNs in the input image outside the bundle essentially get dilated by the cubic interpolator, eroding the bundle; this is also why nearest-neighbour interpolation mitigates the issue.

---

Otherwise, +1 for streamlines transformation (if it fits with your wider experiment).

[ThijsDhollander]

@fionaEyoung

This is a good workaround. For some reason I was reluctant to transform the streamlines on account of tcktransform only accepting a warp image instead of a transformation matrix, but I bit the bullet and the results look good.

Excellent. Yes, the theoretical difference is likely not huge, but it’s a win-win: you avoid any issues of the kind you had before, and it’s better regardless. You should be fine.
On the side, because it had been challenged somewhere above: I do see several very good purposes for performing the normalisation that you’re doing here. If you’ve got any questions about TODs and what can / cannot make sense, just let me know. Otherwise, I think you’re likely well on top of what you’re intending to do.

Cheers & take care,
Thijs

[fionaEyoung]

@rsmith

For voxels where the value of tod0.mif is 0 (i.e. no intersecting streamlines), the value in image todnorm.mif will be NaN due to division by zero.

Oh, of course…! So mrtrix uses 0/0=NaN, I know mathematically that’s true but somehow I just expected everything outside the tract to remain zero. ¯ \_(ツ)_/¯

Thank you all for your inputs, if only I could mark multiple posts as solutions I would.