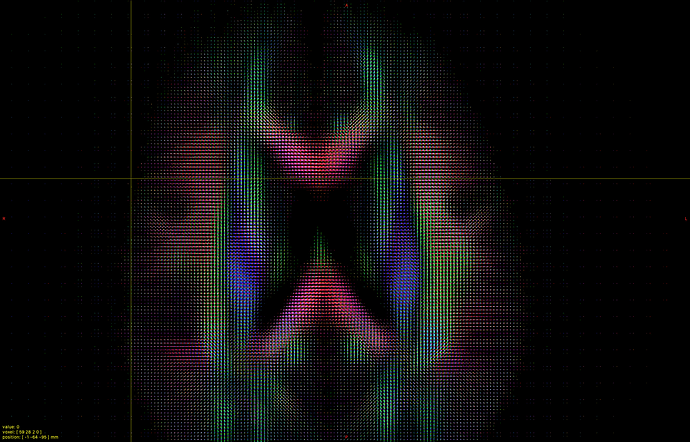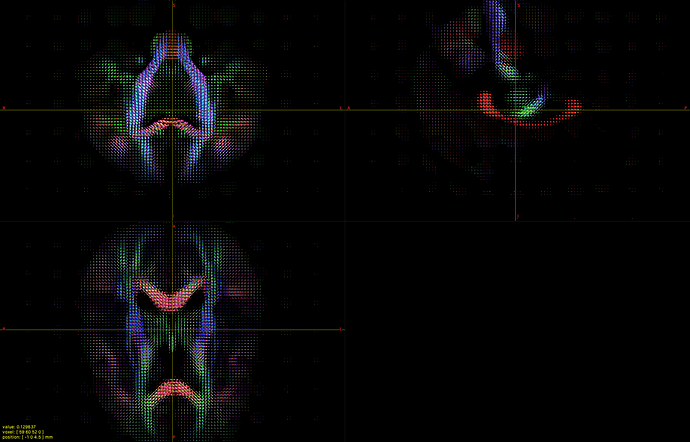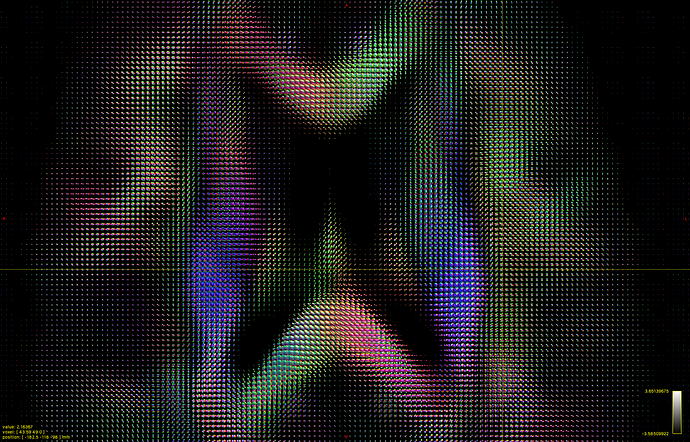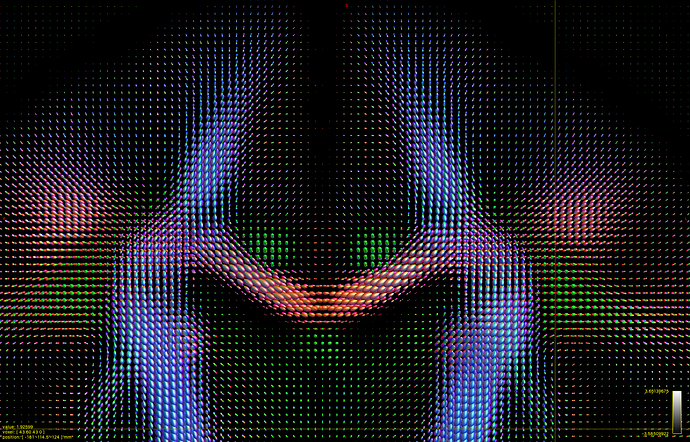Wrong FOD orientations

dpecheva · June 26, 2020, 8:05am

hello,

i am working with some slightly problematic data that is stored solely as the SH coefficients in 4D matrix in matlab format (sh_mat = 120x120x100x15 matrix) and i am trying to convert it to .mif using the write_mrtrix command. the data has a transform associated with it

M =	-2     0     0   122
     0    -2     0   122
     0     0    -2   102
     0     0     0     1


fod.data = sh_mat; 
fod.transform = M;

and write_mrtrix(fod, 'outfod.mif') gives the wrong orientation in the corpus callosum (obv they’re all wrong but it’s noticeable in the CC). you can also see it in the projections to the cortex.

I’ve tried a bunch of different ways to flip the orientations but nothing’s worked, any suggestions on this would be great.

thanks!

maxpietsch · June 26, 2020, 8:52am

Hi Diliana,

It looks like your gradient table and DWI image do not match so you’d need to look into your acquisition and processing pipeline. dwigradcheck might be handy.

Unrelated but the determinant of your transformation matrix M is negative, meaning you’re flipping your image.

Cheer,
Max

jdtournier · June 26, 2020, 9:53am

I think the issue might be related to those negative entries on the diagonal of your transform – as @maxpietsch pointed out. There’s a good chance that’ll flip all the axes. Have you tried making all of those positive?

Otherwise, where do these data come from? If they’re using different conventions from MRtrix, we’d need to take a close look at what these are. There’s a lot of ways this information can be represented - even if it is all valid SH coefficients…

dpecheva · June 26, 2020, 6:09pm

Hi Donald and Max

So making it positive does not help:

so the data are an average fod. SH coeffs of individual subjects are estimated in native space using in-house code for RSI (this is the original paper) then subjects are registered together using a tensor registration and the native space SH are transformed to the common space and average, and the average is what i’ve got here. the registration/transformation/averaging is done by someone else so i don’t know the details but will find out (all this processing has been done before me/by other people)

but i see the same problem when i try to convert subjects native space SH to .mif, so before any transformation of the data which makes me think it’s more about how the data are stored. also i did a quick check to see what i get using dwi2fod, expecting if there was a problem with the gradients that the fod orientations would again be messed up, but that looks correctly orientated.

dpecheva · June 26, 2020, 6:12pm

also i wanted to say this but it only would let me post one image:
i probably should have mentioned this earlier but when i get the data if i just do write_mrtrix the on the sh_mat as is i get:

but re-ordering the SH indexing to 1 6 5 4 3 2 15 14 13 12 11 10 9 8 7 gives me what i showed in the first post.

jdtournier · June 26, 2020, 6:23pm

Ok, then I’m assuming the issue is indeed that our SH storage conventions differ from the package you’re using – it certainly seems like the order is different, since you’ve already dealt with that. The remaining issues might relate to inverting some of coefficients or something like that – for instance, there’s a (-1)^m term (the Condon–Shortley phase) that features in some conventions but not others. The way we combine the complex SH terms to form a real basis (sometimes called the tesseral spherical harmonics) might also assume different conventions. Lots of ways things can end up defined differently… Maybe if you can find the exact definitions assumed in their code, we can figure out the mapping between the two?

dpecheva · June 30, 2020, 1:28am

success! i think… looking at the original maltab code

for l = 0:2:order
  p = legendre(l,cos(Theta)');
  for m = -l:l
    j = (l^2 + l + 2)/2 + m;
    if m<0
      c1 = factorial(l-m)/factorial(l+m);
      c2 = (2*l+1)/(4*pi);
      c3 = (-1)^(abs(m))*(factorial(l-abs(m))/factorial(l+abs(m)));
      Ylm = sqrt(c1*c2)*c3*p(abs(m)+1,:)'.*exp(i*m*Phi);
      Y(:,j) = sqrt(2)*real(Ylm);
    elseif m>0
      c1 = factorial(l-m)/factorial(l+m);
      c2 = (2*l+1)/(4*pi);
      Ylm = sqrt(c1*c2)*p(m+1,:)'.*exp(i*m*Phi);
      Y(:,j) = sqrt(2)*imag(Ylm);
    else
      c1 = factorial(l-m)/factorial(l+m);
      c2 = (2*l+1)/(4*pi);
      Ylm = sqrt(c1*c2)*p(m+1,:)'.*exp(i*m*Phi);
      Y(:,j) = Ylm;
    end
  end
end

the m<0 term has a (-1)^(abs(m)) so multiplying the negative degree coefficients by (-1)^(abs(m)) gives (apparently) correct orientations.

but to be honest i don’t really understand the c3 term for m<0.

jdtournier · June 30, 2020, 1:35pm

Good to hear!

Me neither… But there’s a lot of redundancy in this code. I reckon this would do the same job:

for l = 0:2:order
  p = legendre(l,cos(Theta)');
  for m = -l:l
    j = (l^2 + l + 2)/2 + m;
    c1 = factorial(l-abs(m))/factorial(l+abs(m));
    c2 = (2*l+1)/(4*pi);
    Ylm = sqrt(c1*c2)*p(abs(m)+1,:)'.*exp(i*m*Phi);
    if m<0
      Y(:,j) = sqrt(2)*(-1)^(abs(m))*real(Ylm);
    elseif m>0
      Y(:,j) = sqrt(2)*imag(Ylm);
    else
      Y(:,j) = Ylm;
  end
  end
end

and there’s a good chance that would then match our convention, apart from that (-1)^abs(m) term, and the need to invert m – but to really verify this would require writing a bit of test code…

dpecheva · July 1, 2020, 12:05am

thanks donald! hope all is well back in london!

pya · March 26, 2023, 6:44am

Dear Tournier,

c=     [0.10931488, -0.01913602, -0.10427029,  0.07533529,  0.02588572,
       -0.06559721,  0.01725084,  0.03923653, -0.02286121, -0.04493933,
       -0.00923942,  0.00201445, -0.07635243, -0.04356742,  0.02039322,
       -0.00857603, -0.01146724,  0.01803261,  0.01759768, -0.00576732,
       -0.01670703,  0.00723215, -0.0077153 , -0.00871654, -0.02096124,
        0.02479116,  0.02442713, -0.00403376,  0.0023532 ,  0.00225714,
       -0.00634937, -0.00323842,  0.00272784,  0.00499127, -0.00106389,
       -0.0041335 ,  0.00481908, -0.0025849 ,  0.00145664, -0.00031923,
        0.00514136,  0.00942071, -0.00342335, -0.00609509, -0.00026663];
    cc=reshape(c',[1,45]);
dx = pi/60;
% dx = pi/30;
col = 0:dx:pi;
az = 0:dx:2*pi;
[Phi,Theta] = meshgrid(az,col);
for l = 0:2:8
  p = legendre(l,cos(Theta)');
  for m = -l:l
      clear v
      j = (l^2 + l + 2)/2 + m;
    if m<0
      c1 = factorial(l-m)/factorial(l+m);
      c2 = (2*l+1)/(4*pi);
      c3 = (-1)^(abs(m))*(factorial(l-abs(m))/factorial(l+abs(m)));
      v=reshape(p(abs(m)+1,:),[size(exp(1i*m*Phi),1),max(size(p(abs(m)+1,:),1),size(p(abs(m)+1,:),2))/size(exp(1i*m*Phi),1)])
      Ylm = sqrt(c1*c2)*c3*v.*exp(1i*m*Phi);
      Y{j} = sqrt(2)*real(Ylm);
    elseif m>0
      c1 = factorial(l-m)/factorial(l+m);
      c2 = (2*l+1)/(4*pi);
      v=reshape(p(abs(m)+1,:),[size(exp(1i*m*Phi),1),max(size(p(abs(m)+1,:),1),size(p(abs(m)+1,:),2))/size(exp(1i*m*Phi),1)])
      Ylm = sqrt(c1*c2)*v.*exp(1i*m*Phi);
      Y{j} = sqrt(2)*imag(Ylm);
    else
      c1 = factorial(l-m)/factorial(l+m);
      c2 = (2*l+1)/(4*pi);
      v=reshape(p(abs(m)+1,:),[size(exp(1i*m*Phi),1),max(size(p(abs(m)+1,:),1),size(p(abs(m)+1,:),2))/size(exp(1i*m*Phi),1)])
      Ylm = sqrt(c1*c2)*v.*exp(1i*m*Phi);
      Y{j} = Ylm;
    end
  end
end
all=zeros(61,121);
for q = 1:45
all = all+c(q)*Y{q};
end
      [Xm,Ym,Zm] = sph2cart(Phi, pi/2-Theta,all);
      surf(Xm,Ym,Zm)

I hope this email finds you well. I am writing to seek your assistance regarding generating a visual FOD using 45 SH coefficients in Matlab.

I have already read the 45 SH coefficients in dimension 4 of the FOD, but I am unsure of how to use them to create a visual representation of the FOD in Matlab. As such, I am hoping that you could provide me with some guidance on how to go about this process.

Could you please advise me on the steps I should take to generate a visual FOD in Matlab using these 45 SH coefficients? It would be greatly appreciated if you could also provide me with any relevant code or resources that could help me with this task.

Thank you very much for your time and expertise. I look forward to hearing from you soon.

Best regards,

Ang

jdtournier · March 27, 2023, 12:09pm

HI @pya,

Probably the easiest thing would be to use my original CSD MatLab implementation, which you’ll find here on Github. The README should be simple enough to step through, but let me know if that’s not what you were after.

All the best,
Donald

pya · March 28, 2023, 2:08am

The FOD was successfully generated with your code, thanks!