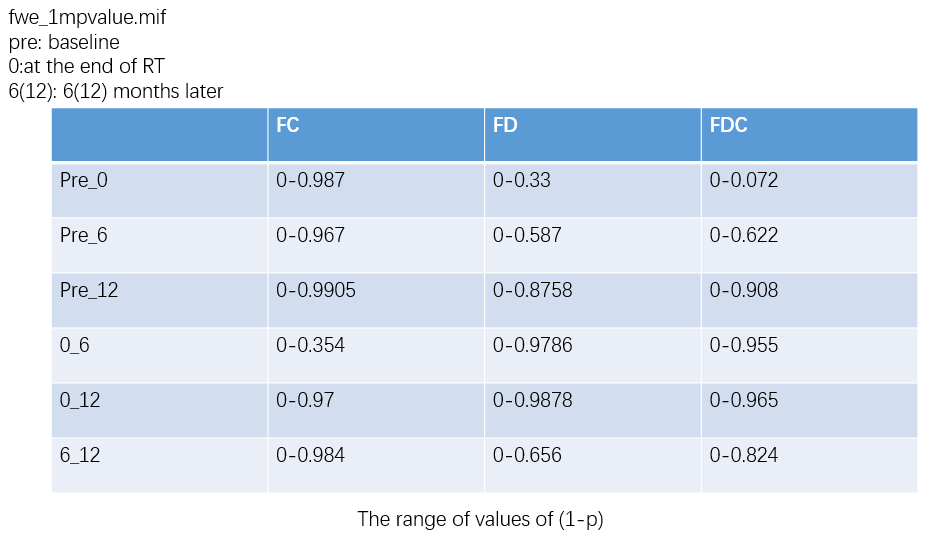
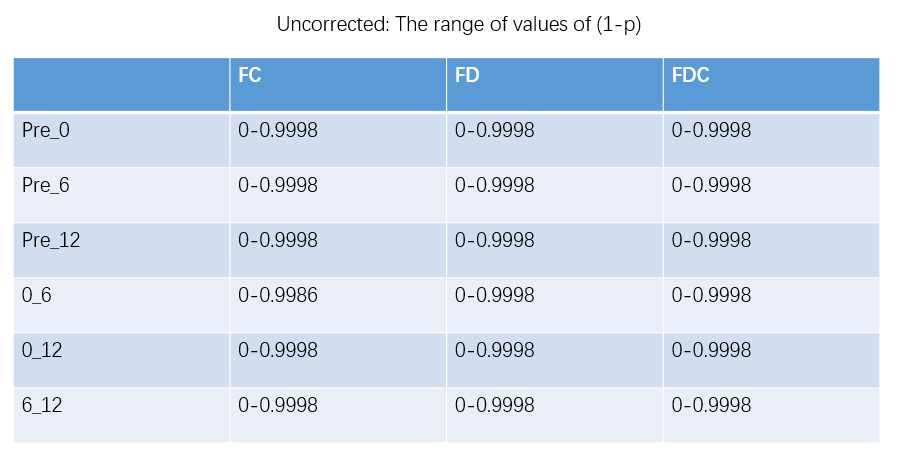
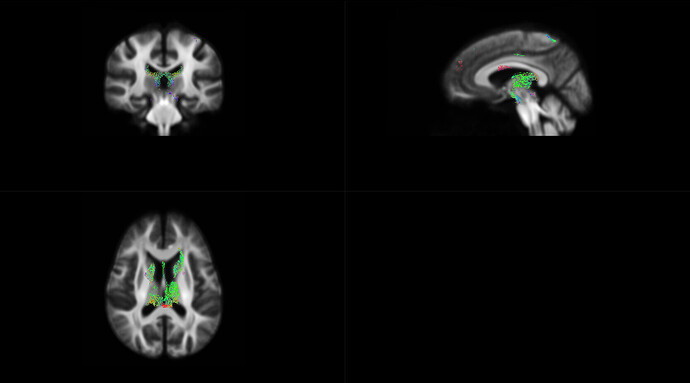
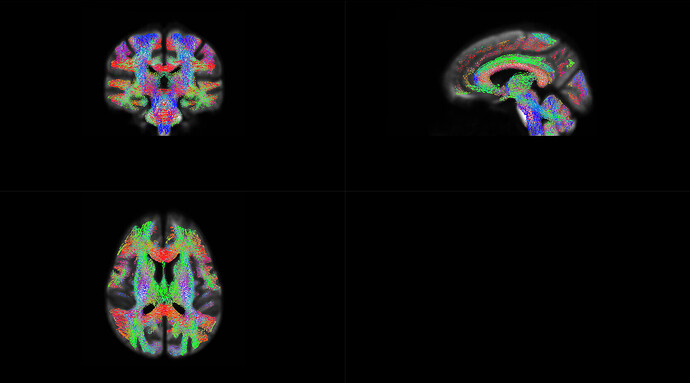
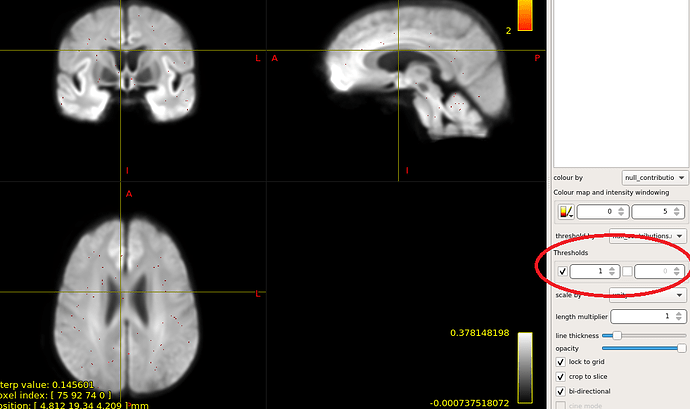
OK,I check the “null_contributions.mif”.And,as shown in the figure below,when I compared FD value between pre-therapy and 12 months after ending therapy,I can find a small number of fixels with large values,e.g. maximum value is 16.
Well, if it’s just one fixel with a value of 16, it might not be a problem. If you had 200 fixels with a value of 16, that would be a problem.
What is the problem?
Was trying to avoid this 
Let’s say hypothetically that there’s “something wrong” with the statistical enhancement algorithm. For some reason, even when the data are being shuffled, one troublesome fixel consistently gets extremely high statistical enhancement values. For each shuffle, it is the maximal enhanced statistic anywhere in the image that is contributed to the null distribution (this is what guarantees familywise error rate control). So this one fixel contributes to the null distribution on every single shuffle (and it would therefore have a value of 5000 in this fixel data file). You now have a null distribution with extremely large values. When you don’t shuffle the data and test your actual hypothesis, the rest of the fixels in your image can’t receive enough statistical enhancement to exceed the 95th percentile of this null distribution and therefore be labelled as statistically significant. So you end up with no statistically significant fixels and don’t know why.
Why might such a thing happen?
Well, imagine that you are using empirical non-stationarity correction using this method, which is activated using the -nonstationarity option. The purpose of this is to try to provide homogeneous statistical power throughout the whole template, rather than having more statistical power in some regions than others purely due to their location in the template. Without going into all of the details, it works something like this:
-
Characterise how much statistical enhancement different fixels receive by chance; i.e. even when there’s no effect in the data (achieved via shuffling), some fixels will still get more statistical enhancement than others.
(This is referred to as the “empirical statistic”)
-
When performing CFE on your actual data (and indeed also while generating the null distribution), whatever enhanced statistics are generated, divide these values by those calculated in step 1 in order to correct for those differences in how much statistical enhancement they receive.
Now if all is well, this method works entirely reasonably. The problem with taking this method from voxel-based stats and utilising it in fixel-wise stats is that it is far more likely to be the case where there are fixels in the template that are entirely disconnected from the rest of the template, due to the FOD template tractogram not intersecting them with any streamlines. These fixels obtain tiny “enhanced” statistic values (which aren’t actually enhanced by any other fixels at all) in step 1. What happens when you divide a number by a tiny value? 
Now isn’t this doing exactly what it’s supposed to? Those disconnected fixels have very poor statistical power due to receiving no statistical enhancement, and so it makes sense that they should be “boosted” by the empirical non-stationarity correction.
Now consider what happens when you have many such fixels, and you are shuffling your data in the generation of a null distribution. By chance alone, it’s likely that one of those fixels is going to acquire a moderately large test statistic value, which is going to be blown out of proportion by the non-stationarity correction. That’s then the maximal value that’s going to be taken from the data and appended to the null distribution for that shuffle. And this happens for every shuffle, because you have a large number of disconnected fixels, and on every shuffle, purely by chance one of them is going to obtain a large test statistic. So you end up with a null distribution with extremely large values, and when you threshold your actual data at whatever enhanced test statistic corresponds to p=0.05 you don’t see anything.
This is I believe why a number of people have reported that “paradoxically” their statistical results are reduced when using non-stationarity correction. I suspect it’s not actually paradoxical in many instances, it just requires looking at the data a little more closely. My figuring out what was going on here is the reason why fixelcfestats now outputs the null_contributions.mif image every time.
Okay. But you’re not using empirical non-stationarity correction, right? So why is this concern being raised? Well, you’re not using empirical non-stationarity correction; but you are almost certainly using intrinsic non-stationarity correction. When you look at the expression in that abstract, there’s similarly a term in the denominator that’s based on fixel-fixel connectivity. If that term is exceptionally small for some fixels, there’s the prospect of a similar effect occurring. This is why many users will have noticed a new warning message in fixelcfestats talking about disconnected fixels being excluded from statistical inference: that’s me trying to mitigate this issue. With this basic threshold in place, in my own experience this overall effect does not manifest to the same extent using intrinsic non-stationarity correction as what it does with the empirical non-stationarity correction technique; but there is always the chance that in somebody else’s data that it may manifest, and they will then come on here complaining that FBA doesn’t produce good results… 
Using a fixel mask for statistical inference that excludes fixels that don’t possess enough fixel-fixel connectivity would be preferable, and I intend to modify the documented pipeline to include this. One can currently use tck2fixel to get a streamline count per fixel and threshold that, and in 3.1.0 it should be possible to do such thresholding based on the extent of fixel-fixel connectivity, which is maybe a more tailored solution.
TL;DR: If the values in that “null contributions” image are not scattered approximately homogeneously throughout the template, but there are instead a small number of fixels with large values, you’re not getting as much statistical power as you could.
Cheers
Rob