Hi everybody,
I’ve been trying to use mrregister to register some of my patient fod data onto the IIT HARDI template. I posted something similar a week ago, but I didn’t get any responses (Mrregister and the IIT HARDI template), yet I realize the answer is not obvious, and you are not the creators of the IIT HARDI template.
Since my last post, I’ve been trying a couple of things to figure this out, and I’ve also upgraded and redone some preprocessing with the new MRtrix version 3.0 (dwi2response, dwi2fod - thank you again! Version 3.0 dwi2response gives nan)
Here are a couple other results to show how weird this is getting.
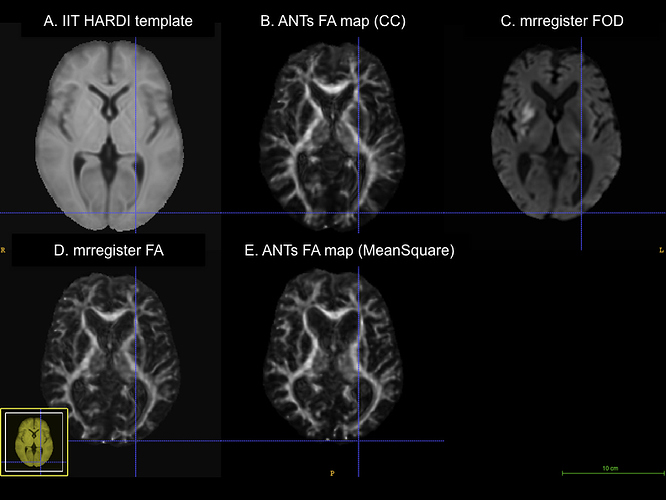
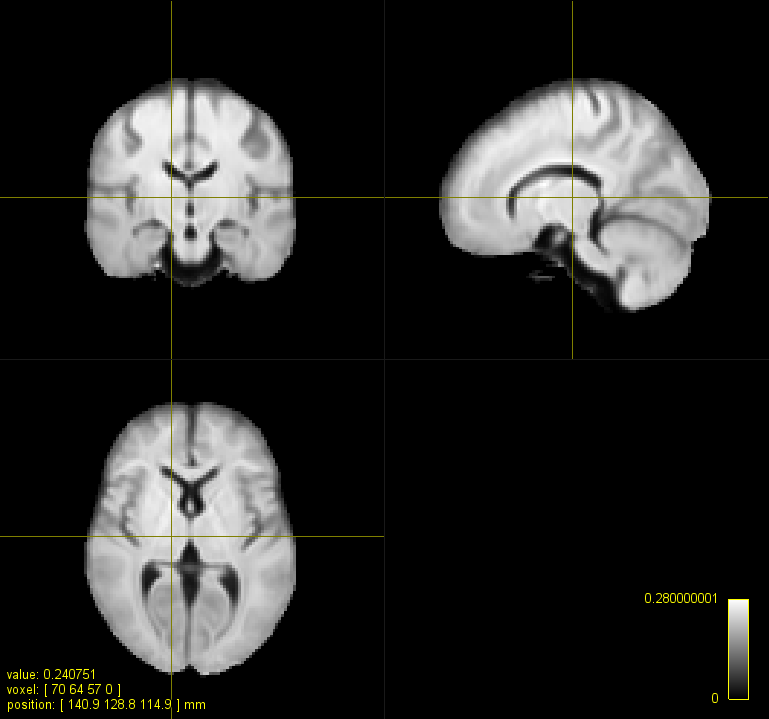
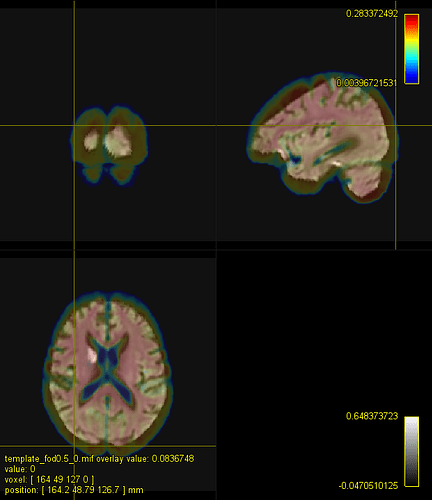
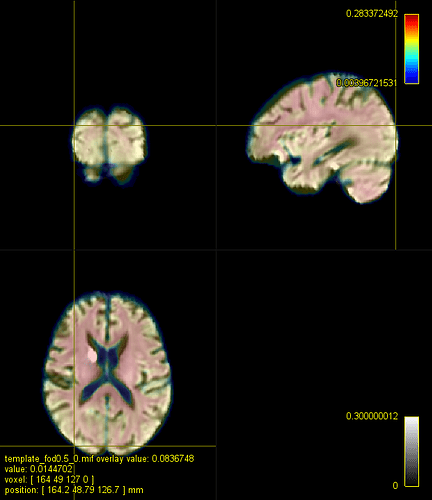
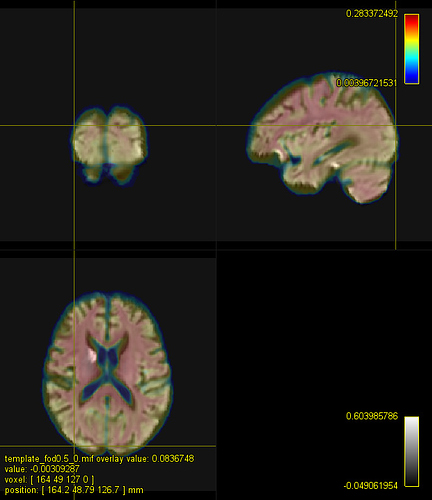
Here is a figure of some registered images along with the IIT HARDI template. The cursor is on the same voxel on all of the images.
A. IIT HARDI template
B. A registered FA map onto the IITmean_FA template using ANTs and the cross-correlation metric for the non-linear registration
C. A registered FOD map onto the IIT HARDI template
D. A registered FA map onto the IITmean_FA template using mrregister
E. A registered FA map onto the IITmean_FA template using ANTs and the Squared Difference metric for the non-linear registration like in mrregister
Here are the commands that I used to perform the registrations in B-E
B.
antsRegistration --verbose 1 --dimensionality 3 --output [dti_FA_,dti_FA_Warped.nii.gz,dti_FA_InverseWarped] --interpolation Linear --winsorize-image-intensities [0.005,0.995] --initial-moving-transform [IITmean_FA_256.nii.gz,dti_FA.nii.gz,1] --transform Rigid[0.1] --metric MI[IITmean_FA_256.nii.gz,dti_FA.nii.gz,1,32,Regular,0.25] --convergence [1000x500x250x100,1e-6,10] --shrink-factors 8x4x2x1 --smoothing-sigmas 3x2x1x0vox --transform Affine[0.1] --metric MI[IITmean_FA_256.nii.gz,dti_FA.nii.gz,1,32,Regular,0.25] --convergence [1000x500x250x100,1e-6,10] --shrink-factors 8x4x2x1 --smoothing-sigmas 3x2x1x0vox --transform SyN[0.1,3,0] --metric CC[IITmean_FA_256.nii.gz,dti_FA.nii.gz,1,4] --convergence [100x70x50x20,1e-6,10] --shrink-factors 8x4x2x1 --smoothing-sigmas 3x2x1x0vox -x [IIT_mean_tensor_mask_256.nii.gz, dti_FA_mask.nii.gz] --float 0 --collapse-output-transforms 1 --use-histogram-matching 0
C.
mrregister fod_wm.nii.gz IIT_HARDI_256_lmax4.nii.gz -force -transformed fod_wm_Warped.nii.gz -nl_warp fod_wm_Warp.nii.gz fod_wm_InverseWarp.nii.gz -mask1 fod_wm_mask.nii.gz -mask2 IITmean_tensor_mask_256.nii.gz
D.
mrregister dti_FA.nii.gz IITmean_FA_256.nii.gz -type rigid_affine_nonlinear -force -transformed dti_FA_Warped_mrregister.nii.gz -mask1 dti_FA_mask.nii.gz -mask2 IITmean_tensor_mask_256.nii.gz -rigid_scale 0.125,0.25,0.5,1.0 -rigid_niter 1000,500,200,100 -affine_scale 0.125,0.25,0.5,1.0 -affine_niter 1000,500,250,100 -nl_scale 0.125,0.25,0.5,1.0 -nl_niter 100,70,50,20 -nl_grad_step 0.1
E.
antsRegistration --verbose 1 --dimensionality 3 --output dti_FA_SD_ --interpolation Linear --winsorize-image-intensities [0.005,0.995] --initial-moving-transform [IITmean_FA_256.nii.gz,dti_FA.nii.gz,1] --transform Rigid[0.1] --metric MeanSquares[IITmean_FA_256.nii.gz,dti_FA.nii.gz,1,NA,Regular,0.25] --convergence [1000x500x250x100,1e-6,10] --shrink-factors 8x4x2x1 --smoothing-sigmas 3x2x1x0vox --transform Affine[0.1] --metric MeanSquares[IITmean_FA_256.nii.gz,dti_FA.nii.gz,1,NA,Regular,0.25] --convergence [1000x500x250x100,1e-6,10] --shrink-factors 8x4x2x1 --smoothing-sigmas 3x2x1x0vox --transform SyN[0.1,3,0] --metric MeanSquares[IITmean_FA_256.nii.gz,dti_FA.nii.gz,1,NA,Regular,0.25] --convergence [100x70x50x20,1e-6,10] --shrink-factors 8x4x2x1 --smoothing-sigmas 3x2x1x0vox -x [IIT_mean_tensor_mask_256.nii.gz,dti_FA_mask.nii.gz] --float 0 --collapse-output-transforms 1 --use-histogram-matching 0
B represents the typical registration using antsRegistration.
C represents the typical registration using mrregister for fod images
D represents the typical registration using mrregister for FA images (and I also added an additional scaling level and changed the gradient step to see if it would be closer to the registration in B)
E represents the antsRegistration using the MeanSquares metric instead of the Mutual Information for the rigid+affine steps and the Cross-Correlation for the Non-Linear Steps.
What seems to be aligning my images best so far - that is, visually - is antsRegistration. It respects the size of my FA maps and really aligns them well with the IITmean_FA template. When registering the same subject’s FOD maps with mrregister, I am unable to get a registered FOD map that is of the same size as the template; however, the deep subcortical white matter structures are well aligned (corpus callosum, corticospinal tract, inferior fronto-occipital fasciculus, superior longitudinal fasciculus, etc.). Moreover, when I use mrregister to register the scalar FA maps, I get a pretty bad registration, and the final size of my image looks like my registered fod map with mrregister. Finally, when I use antsRegistration with the MeanSquares metric, I get something that approaches what mrregister does (although it’s not exactly the same).
As you can imagine, I am really stumped. I would really appreciate any help possible. Please let me know if you have any other suggestions. I would also be willing to send the preprocessed dwi images along with the gradient table if anyone would like to try seeing what they get.
Thanks again for all of your help,
Eric