This wiki post aims to introduce the concepts and terminology associated with modifications of the voxel grid of an image and with changing the real-world location of its content and to highlight related tools within MRtrix3.
TL/DR
In image regridding, the grid of the image data is modified but the relation between the content of the image and the real-world location is preserved. Regridding entails interpolation which can cause a loss of information and introduce bias between images if performed asymmetrically.
Registration tries to find the mapping (transformation, warp) between the content of images, in our case using their real-world locations. The transformation is the process of applying this mapping to propagate information between spaces. It can be performed on images or tractograms. Image transformation can imply regridding to the grid of the target space but this may not always be required or desirable. A linear transformation can be performed without regridding by modifying the (linear) mapping between voxel and real-world locations stored in the image header.
Image data
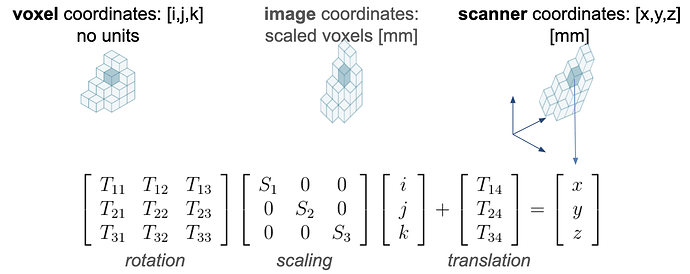
Image data is essentially a block of memory and associated metadata that allows interpreting its content. When we talk about voxels, we refer to the atomic entities of the data array, typically viewed as a regular 3D or higher dimensional grid of unitless data. Voxel-wise operation such as averaging two contrasts of the same image (mrmath, mrcalc) are not concerned with the associated size of voxels or their location in the real world.
In medical image data, each voxel has an associated scaling (inversely related to resolution) that specifies the size and shape (in mm) of the content of each voxel in the real world. Also, the image metadata typically (implicitly or explicitly) contains a 3x3 matrix* that defines the orientation of the voxel grid and the location of the first voxel as an anchor point. We call this rotation and translation information the transformation matrix; see here for more details and how this information can be extracted using mrinfo.
Regridding: resampling with interpolation
When the image grid needs to be changed, for instance, to change the resolution of an image, it is not sufficient to modify the scaling factors. To conserve the association between voxel locations (i,j,k) and the real world location (x,y,z) one needs to adjust the transformation matrix but, more importantly, also the existing voxel data needs to be modified to fit the new voxel grid. The latter requires interpolation to estimate the values of the data at the new grid locations from the ones it was sampled on. This is generally not a lossless process and can lead to artefacts, most commonly “ringing, aliasing, blocking, and blurring”.
Let’s assume we wanted to compute the voxel-wise average of two images that are aligned in scanner space but whose voxel grids are not aligned. To be able to perform voxel-wise comparisons, one or both of the images need to be regridded to a common image grid.
$ mrmath T1.mif T2.mif mean mean.mif
mrmath: [ERROR] Dimensions of image 2 T2.mif do not match those of first input image T1.mif
The command mrgrid can be used for this purpose. For instance, to resample image T1.mif using linear interpolation to match the voxel grid, scaling and transformation of image T2.mif (without changing the scanner-space location of its content):
$ mrgrid T1.mif regrid -template T2.mif T1_regridded.mif -interp linear
$ mrmath T1_regridded.mif T2.mif mean mean.mif
mrmath: [100%] computing mean across 2 images
Image grid manipulations without interpolation
An image grid can be changed without regridding or interpolation, for instance when cropping or padding the image. This process preserves the information stored in the voxels that were part of the image before this operation and does not modify their associated scanner space location. See mrgrid's help page for usage examples of cropping or padding images in any dimension or to the maximum extent of a mask or to the grid of a reference image.
Registration
The purpose of image registration is to calculate the mapping that brings the content of images into alignment. It is possible to register two images without changing any of the images used for the registration if the mapping is all that one is interested in. Typically finding this mapping entails establishing point-wise correspondence of anatomy (but can also be used to ensure functional correspondence). Image registration and analysis of the mapping or of the transformed images allows detecting local changes such as lesions or atrophy in repeat scans, the creation of normative spaces or templates or aligning subjects to these spaces.
The workhorse for image-to-image registration within MRtrix3 is mrregister. population_template can be used to create templates from multiple images. Below is an example of how to nonlinearly register image s.mif with image t.mif which creates the two warps that map between the images :
mrregister s.mif t.mif -type affine_nonlinear -nl_warp W_s2t.mif W_t2s.mif
Note that mrregister currently only supports a least-squares metric which is not well suited for registration across-modalities. If you need to troubleshoot your registration, have a look in the commands help page, here in the community, and at a worked example of challenging data here. The most common sources for problems are related to no or poor masks and different intensity scaling.
We also offer tools to convert linear transformations from Fsl flirt and nonlinear transformations generated from ANTs or any registration software that can transform NIfTI files.
Warping images (and tracks files)
The command mrtransform applies a spatial transformation to images, its purpose is to modify the scanner-space location of the image content.
Linear transformations can be applied directly (if they are rigid (translation and rotation) – only .mif files support this for affine transformations) to the image header. This means that the voxel grid does not need to be changed and no loss of information due to interpolation occurs at this step. However, similarly to mrgrid (see above), mrtransform supports the -template option to resample the image to a target grid.
Applying the transformation that maps the content of image s.mif into the space of image t.mif and regrids it onto the grid of t.mif can be done with:
mrtransform s.mif -warp W_s2t.mif s_at_t.mif -template t.mif -interp sinc
Here, -template t.mif is optional as mrtransform defaults to using the image grid of the warp which is, in this case, identical to that of t.mif.
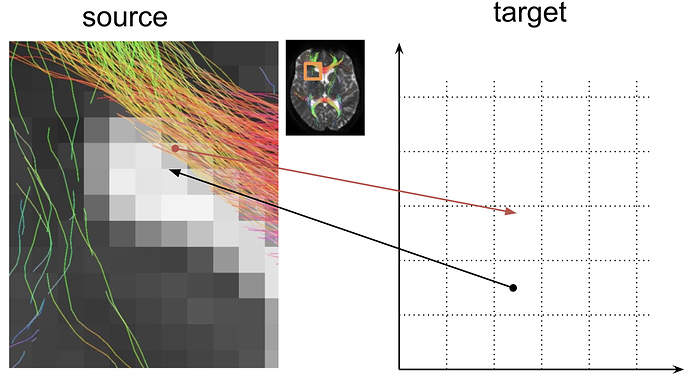
Behind the scenes, mrtransform creates a target grid that is to be used as the output image (s_at_t.mif) and, for each voxel in the target image, uses the warp W_s2t.mif to look up the corresponding location in the source image (s.mif) from which the source intensity value is obtained, in the above example via sinc interpolation, and written to the output image. This is illustrated above, where the black arrow head points at the source location from which the information is obtained via interpolation and pulled into the arrow base in the target grid.
Similar to image intensity values, streamlines can be moved between spaces. tcktransform is our tool that performs this operation. Note that warping tractograms differs due to the type of information stored. Streamlines, consist of a series of coordinates (vertices, defined in source space) that need to be pushed to new locations in the target space. In contrast, image information needs to be pulled to the target grid. The two operations have different spatial lookup spaces (target for images, source for tracks) and (approximately) opposing offset directions (see red arrow above). Therefore, compared to warping images, you will need to apply the inverse transformation to warp tracks files from source to target space.
tcktransform currently does not support linear transformation files but linear transformations can be converted to warps as shown in this worked example of warping streamlines to target space.