Troubles with tractography on 7T diffusion data

gmkerbler · December 12, 2016, 8:11am

Hi MRtrix team,

I have recently collected DWI data on a 7 Tesla Siemens scanner. I realise 7 T is not optimal for DWI, but the plan is to collect other modalities that benefit from the high resolution at high field, and collect DWI along for all the participants.

Now, I had a closer look at the data, and the quality, I’m afraid, seems to be very bad.
We collected the following data:

b=1000, 30 directions (2x b0’s), 1.5 x 1.5 x 1.7 mm(3)

b=2500, 64 directions (4x b0’s) 1.5 x 1.5 x 1.7 mm(3)

I’ve done the ‘Basic DWI Processing’ on the latter (b=2500), using csd and tournier algorithm (with automatically selected lmax=4), and created a wholebrain 100K.tck (not using ACT).
Apart from distortions (e.g. frontal lobe; which can be dealt with OK by TOPUP) and signal drop out in the temporal lobes, there are the following problems:

1) Gradient directions seem to be poorly distributed:

$ dirstat enc.b 
enc.b [ 64 volumes ]

b = 0 [ 4 directions ]

  Bipolar electrostatic repulsion model:
    nearest-neighbour angles: mean = 90, range [ 90 - 90 ]
    energy: total = inf, mean = inf, range [ 1.79769e+308 - inf ]

  Unipolar electrostatic repulsion model:
    nearest-neighbour angles: mean = 90, range [ 90 - 90 ]
    energy: total = inf, mean = inf, range [ 1.79769e+308 - inf ]

  Spherical Harmonic fit:
    condition numbers for lmax = 2 -> 0:


b = 2497.42 [ 60 directions ]

  Bipolar electrostatic repulsion model:
    **nearest-neighbour angles: mean = 10.8169, range [ 3.12222 - 23.3815 ]**
    energy: total = 11649.6, mean = 194.161, range [ 99.686 - 477.799 ]

  Unipolar electrostatic repulsion model:
    nearest-neighbour angles: mean = 14.3701, range [ 3.94214 - 33.1807 ]
    energy: total = 6336.11, mean = 105.602, range [ 36.237 - 277.73 ]

  Spherical Harmonic fit:
    condition numbers for lmax = 2 -> 8: 1.42623 2.00688 3.99685 12.7592

2) Response function looks very strange:

3) Single fibre mask looks very poor (here on an axial slice at the level of the corpus callosum crossing the midline):

4) And finally, the resulting tracks look noisy, short and directionality is bad (probably obvious given all the previous troubles):

As you can see, they don’t even cross the midline via the corpus callosum (even the FA is very noisy at that spot).

I realise, my post probably reads like a paper I could title with ‘Why you shouldn’t do diffusion imaging at 7 Tesla’, however I think there were some mistakes made in the initial sequence design (i.e. directions scheme). Now I’m wondering whether improving the sequence would greatly improve the quality of the DWI data, or if you guys would suggest to just completely avoid (wholebrain) DWI at 7 T? And instead collect data at 3 T and then do registration between 7T&3T when transferring i.e. ROIs for seeding from fMRI (7T) to DWI (3T)? Given I have two shells, would you suggest to do MSMT-CSD?

Apologies for the long post and thank you all already for your time in discussing this issue!

Best,

Georg

jdtournier · December 12, 2016, 8:50am

Yes, looks like your DW directions are pretty terrible… With 60 DW directions, you should be able to have stable fits all the way to lmax=8, with conditions numbers only slightly larger than one across the range. Yet your conditions number is already above 2 for lmax=4, which is only a 15 parameter fit… I’ve no idea where these directions might have come from, but it’s not that they’ve been optimised assuming a single unipolar point charge (a common problem in the early days), or repeated with the opposite directions (used to be done sometimes for eddy-current compensation). Maybe you’re running on a Philips system with the overplus option…? That one is a true HARDI-killer, avoid at all costs.

So you should definitely be able to do a lot better with improved DW directions. You can use dirgen to generate some if you want, you’d then need to figure out how to import them into your sequence.

The other problems to deal with on these systems are the strong Rician bias, due not to 7T so much as the tendency to run at very high resolutions on these systems, which can mean a lot more noise than at 3T. There is a temptation to use averaging to overcome the SNR loss, but this does nothing to remove the Rician bias - if anything, it just makes it worse by improving the SNR without any compensation for the bias (or to put it another way, the noise is no longer Rician distributed, but non-central Chi distributed - I think). This is definitely worth bearing in mind.

The other problem to worry about is the strong B1 inhomogeneity, which needs to be corrected for. Unlike many other approaches, in MRtrix we don’t normalise to the b=0 image, so this bias field is not inherently factored out.

Hope this helps…

ThijsDhollander · December 13, 2016, 12:15am

Apart from the major issues with that direction set (maybe you could post the full set here, that may give us a bit more insight into what may have gone wrong here), the other thing to take into account if you want to use these data as a whole (multi-shell) dataset, e.g. for MSMT-CSD, would be to check for intensity normalisation in case these were two separate acquisitions (even if they’re both scans in the same session!). A quick check by opening up both and flicking back and forth between a b=0 in both scans while using the same intensity window for both, should give you an idea of whether this is a problem present in your case or not.

It’s definitely something we may have to warn users for in general: I’ve seen quite a few users and collaborators now that try to do a multi-shell acquisition by acquiring separate single-shell (+b=0) scans… I don’t know much about the options other manufacturers offer, but for Siemens, this is their only option (I believe) when they don’t have access to the free mode.

gmkerbler · December 13, 2016, 7:31am

Thanks for your replys @jdtournier @ThijsDhollander

The directions were generated by someone doing the following (excerpt from the method):
"Uniformly distributed gradient directions were generated based on a generalization of the electrostatic energy minimisation technique (Caruyer et al., 2013)"
Here is the content of the enc.b file:

$ cat enc.b 
-0 0 0 0
-0 0 0 0
-0 0 0 0
-0 0 0 0
-0.2360710907 -0.5241581761 0.8182473016 2510.00005
0.8930207995 0.2590059111 0.3680078664 2494.999933
0.796183758 -0.1290299516 0.5911367821 2494.999904
0.2339639331 0.9298547756 -0.2839559373 2495.000009
0.9356857601 0.1399529689 0.3238909149 2504.999982
-0.5058270183 0.8447100248 0.1749399942 2499.999998
-0.3462198908 0.8475387947 -0.4022558623 2485.000019
0.4569682411 -0.6309562881 -0.6269562897 2489.999916
0.4869967891 0.3889968201 0.7819946301 2495.000146
0.6178450023 -0.672831014 0.4068979967 2505.000065
-0.5769842522 -0.1049970313 0.8099782689 2504.999962
-0.8266946096 -0.5208077549 -0.2129208888 2485.000123
0.8937118401 -0.03998698656 0.4468558915 2499.999924
-0.2901009102 -0.5411887877 -0.7892757173 2494.999983
0.1159509877 -0.962590945 -0.24489598 2485.000019
-0.8001819791 -0.4030919746 0.4441009574 2505.000003
-0.513981006 0.8399700052 -0.173994011 2489.999996
0.7885481521 0.1529120438 0.5956590624 2504.999959
-0.9492795986 0.2330689027 0.2110619111 2499.999988
0.232964044 0.7828801665 -0.5769110842 2489.999852
0.02099901373 -0.1879900832 0.9819464191 2504.999912
-0.2169319854 -0.9557008935 -0.1989379701 2489.999954
0.7740032045 -0.6040021819 0.1900010625 2504.999951
-0.1609279725 0.3558399618 0.9205868288 2494.999958
-0.1470350137 -0.7311731116 0.6661580785 2500.000121
0.888141241 0.4170661206 0.1930310522 2504.999844
0.5619707671 0.2319879412 0.7939587219 2505.00007
0.3808088054 -0.1429279377 -0.9135405073 2484.999839
-0.3060000164 -0.199000012 0.9310010662 2500.00012
-0.3320860169 0.1300340071 0.9342430275 2494.999967
0.9632264461 0.2650621285 0.04401001725 2494.999976
0.9595014539 -0.2051071071 0.1931010993 2509.999885
-0.4529648336 -0.8889316854 0.06799498704 2504.999922
-0.7731326352 -0.6281077115 -0.08801494822 2495.000042
0.7090818157 -0.4080468771 0.5750658438 2504.999796
-0.6927691765 0.02399201134 0.72076019 2504.999838
0.6816591122 -0.5287350428 0.5057470803 2505.000128
0.1419950626 0.7249763419 0.6739782681 2494.999853
0.7401682929 0.3880881552 -0.5491251969 2484.99986
-0.1030059935 0.8220439545 0.5600299119 2504.99995
-0.5840369388 -0.5960379968 -0.5510349902 2494.999928
-0.08800798507 0.3350309656 0.9380878672 2495
0.552262842 0.7923768415 -0.2591229329 2489.999945
0.8381576806 0.4580858273 0.2960558684 2510.000028
0.3629950704 -0.5609931044 0.7439901314 2494.999839
0.1840620383 0.3921330914 0.9013061659 2509.99997
-0.7209380612 0.6929410724 -0.008999009316 2489.999815
-0.4331010609 -0.6821590491 0.5891370832 2504.999985
-0.5021139718 -0.6901569473 -0.5211189379 2484.999895
-0.1709440434 -0.5088330741 0.8437221324 2499.999933
0.4629678525 0.422970855 -0.7789457127 2485.000071
-0.3850300767 0.8090640943 -0.4440350564 2484.999976
-0.7131019638 0.2470350147 0.6560939649 2500.000007
-0.2599230923 -0.884737203 0.3868850833 2494.99993
-0.001000001065 0.07700202777 -0.9970304347 2494.999861
-0.03700200945 0.9020573801 -0.4300271321 2479.999983
-0.5703201974 0.3031701358 0.7634282816 2499.999949
0.2821051403 0.1450540626 0.9483543688 2499.999865
-0.7210980484 -0.6080819964 0.3320450125 2499.999992
-0.2669850711 0.9599452178 0.08499500357 2505.00007

Previously I tried to supply an aqcuisition scheme (10x b0, 32dir b1000, 64dir b3000) to the operator for the DWI scan created using your ‘gen_scheme.sh’ script (is ‘dirgen’ the new version of this?), but the format the directions were in was not compliant with the siemens scanner format. The reason being, that they needed to be:
"… (x,y, z) per row, where sqrt(x^2 + y^2 + z^2) =1, and if you want different b-values these values need to be scaled accordingly. So for all direction with b-value 3000 the sqrt must be 1, but for b-value of 1000 it must be 0.33".

Is it possible to just convert the direction set in order to fullfill these criteria? (This might be a trivial issue, apolgies, I’m just not experienced in sequence development)

In regards to the high resolution acquisition resulting in a lot more noise (due to Rician bias), would it then be better to reduce the resolution to i.e. 2.5 x 2.5 x 2.5?

Re: B1 ihnomogeneity correction, does your “dwibiascorrect” script deal with this issue, or is this a whole other problem?

Also, @ThijsDhollander in regards to MSMT-CSD, the different shells have different intensities at the same voxels when flicking between the b0’s in FSLview (while keeping Min/Max the same), is that what you mean?
I know it’s not possible for the Siemens scanner to acquire a reverse-PE b0 in the same acquisition (it has to be a different run), which is also an issue, but I thought at least identical-PE could be acquired in the same acquisition, maybe I’m wrong though…

jdtournier · December 13, 2016, 11:32am

So here’s what that looks like plotted in 3D:

Clearly this is very far from optimal…

This is what you should see (generated using dirgen 60 dir60.txt -cartesian:

with corresponding stats in this case:

$ dirstat dir60.txt 
dir60.txt [ 60 directions ]

  Bipolar electrostatic repulsion model:
    nearest-neighbour angles: mean = 18.9073, range [ 18.114 - 19.9099 ]
    energy: total = 8002.93, mean = 133.382, range [ 131.922 - 135.419 ]

  Unipolar electrostatic repulsion model:
    nearest-neighbour angles: mean = 19.3059, range [ 18.1859 - 31.9532 ]
    energy: total = 3999.4, mean = 66.6566, range [ 40.5186 - 82.3908 ]

  Spherical Harmonic fit:
    condition numbers for lmax = 2 -> 8: 1.00556 1.02185 1.05982 1.20328

Note that the worst condition number for the SH fit is 1.2 at l_max=8, compared to your 12.7592…

So I’m not sure where your directions came from, maybe they were somehow modified along the way? But they’re clearly nowhere near optimally distributed…

No, gen_scheme.sh uses dirgen internally to generate the directions for each shell. I recommend you keep using that script, but figure out how to massage the output into a format suitable for Siemens. Something like this should do it:

bmax=3000
cat dw_scheme.txt | awk '{ n=sqrt($4/'$bmax'); printf "Vector["NR"] = ( "; if (n>0) printf $1*n ", " $2*n ", " $3*n " )\n"; else printf "0, 0, 0 )\n"; }'

This will scale the vectors by sqrt(b/bmax), which is what I think is the right scaling (more on that later), and produce them in a format that can be directly inserted into your DiffusionVectors.txt file. You may need to amend it to fit your needs though, and you’ll also need to insert something like this at the top of the output (again, make sure it fits with what you’ve got):

# multi-shell set, generated using gen_scheme
[directions=106]
CoordinateSystem = xyz
Normalisation = none

So about getting the scaling right for this to work, I note you quoted:

Where does this come from? I’d assume that the right scaling here should actually be sqrt(1000/3000) = 0.57735, not 0.33 - this is what the code in the MRtrix3 backend assumes, and I’m pretty sure we verified this was correct at the time…

That would be a phenomenal waste of resources: this is standard resolution at 1.5T…

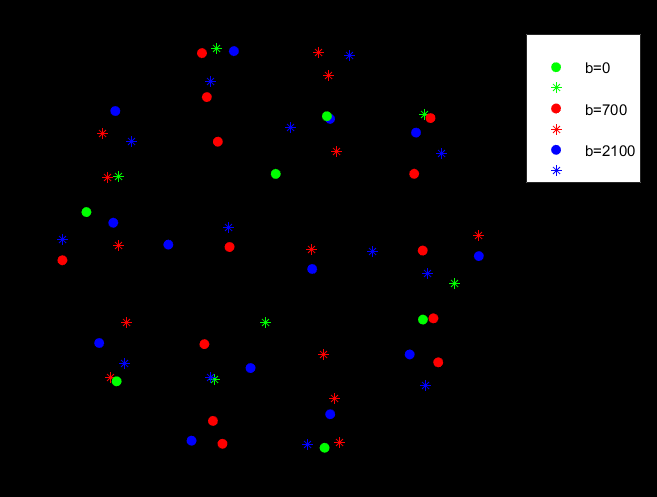
No, you should be able to push the resolution up to maybe 1.8mm isotropic without much of an issue, it’s just that as you lower that, your SNR will drop rapidly, so you’ll need to figure out what works best. You should aim for an SNR in the b=0 image no lower than 15 - bearing in mind that SNR will be strongly spatially variable at 7T, so you’ll need to measure it from the worst location SNR-wise that you care about (most likely the brainstem, in my experience).

Yes, that’s what it’s supposed to do.

Yes, that would definitely be a problem for MSMT-CSD. You can try to scale each acquisition so that the b=0 image intensities match, as long as none of the other acquisition parameters differ between the acquisitions. You can use mrcalc for that, in combination with mrstats to get the b=0 intensities. dwiextract -bzero may also come in handy here. I’d also recommend sticking to within a brain mask to avoid undue influence from the background noise here. This might look something like:

# generate a brain mask (use the same mask for all acquisitions):
dwi2mask dwi.mif mask.mif
# then for each acquisition, get mean b=0 image intensity within mask:
sig=$(dwiextract dwi.mif -bzero - | mrmath - mean -axis 3 - | mrstats - -mask mask.mif -output mean)
# and scale to have mean b=0 signal = 1000:
mrcalc dwi.mif 1000 $sig -div -mult dwi_scaled.mif
# once you've done that for all of them, recombine with mrcat:
mrcat dwi_scaled1.mif dwi_scaled2.mif dwi_scaled3.mif -axis 3 dwi_all_scaled.mif

This is just rough and ready, you’ll no doubt need to amend to suit your data, but that should give you an idea of what you can do…

No, you’re correct. As long as you can provide a DifffusionVectors.txt file to the system in the right format (as above), you should be fine. What @ThijsDhollander what referring to was that this relies on you having the right license in place - it’s not enabled unless you’ve purchased the appropriate diffusion package…

ThijsDhollander · December 14, 2016, 5:44am

Quickly checked it using my own simple Matlab script (sorry @jdtournier, but mine has colours and shading and stuff! ):

(colours just indicate polarity; green are the polarities in the set, red their opposites)

…so yes, that doesn’t look good at all (and is in line with the findings Donald posted about the set as well). I do expect a bit of mess looking at a single shell, but having used Caruyer’s approach: you’ve got to take into account that that approach tries to optimise the spread per shell, but also across shells (I suppose there’s some weighting between both optimisation criteria). I know some people have started using it in practice… not to be too opinionated, but I’m not sure I’m a big fan of it. It does mess up the sets per shell, and it means that even using 60 directions for your b=3000 shell, you may end up with not enough angular resolution in certain areas of the orientational domain (the big gaps in the visualisation above), and angular biases all over the place.

…but even using Caruyer’s approach, I find it hard to believe that this would in and of itself lead to the above, if you’ve only got 30 directions on the only other shell. Some of the angles between certain pairs of directions in the set seem so small that you wouldn’t even get them for a 94 direction set (so even just ignoring optimisation within individual shells, and optimising the whole set of 94, and selecting a random subset of 64, would probably not look this bad). The only way I can see this resulting from anything, is using that approach for more than those two shells, and then afterwards just using only the b=1000 and b=2500 shells from it. But that would indeed just be bad practice, and even your multi-shell data at hand is then practically unusable.

Yep, I can confirm this. It’s the squares of the (L2) norms of your vectors that must scale like the b-values, with the highest b-value just having a unit norm (and then setting that as the b-value of your scan). So for example for a multi-shell acquisition with b-values = 0,1000,2000,3000 your diffusion vector norms as specified in that file should be 0, 0.5773, 0.8165 and 1. The squares of these norms are 0, 0.333…, 0.666… and 1.

Yep, that’s exactly it, and if these intensities differ significantly, it’s something that needs to be fixed. Note this wouldn’t happen if it were a single multi-shell scan, rather than separate scans. Donald’s suggested course of action above is a reasonable starting point to fix it, if it did happen. The b=0 images are your friends here, as they’re the only common contrast between both scans.

If your (Siemens) software is up to date, messing with this file is no longer needed (and I would discourage it, since you may end up removing other important schemes in there, or messing up the file by including multiple schemes with the same number of directions). You can now save this as a file with any name (preferably ending in the .dvs extension), and after selecting the free mode, the interface should allow you to load such a file and consequently select a number of directions. The [directions=...] line in your scheme acts as both the actual number as well as an identifier for selecting your scheme here. A given .dvs file (this also applies to the default DiffusionVectors.dvs) can not have any two schemes with the same number of directions. We used to alter the number of b=0 images to deal with this limitation, but with the introduction of allowing to load your own files, this is no longer an issue.

Yep, so just to be clear: you need the correct license to have access to the free mode. The free mode allows to configure your own schemes, which inherently allows for multi-shell scans using the format and scaling of the vectors we discussed. The free mode (currently, and as far as I know) doesn’t allow multiple phase encoding directions in a single scan, so that still requires a separate scan indeed.

jdtournier · December 14, 2016, 8:43am

Guess I’m not up to date either then…

Good to hear about these latest changes, sounds like it does make things easier to manage. I assume the format within the file is as before…? I.e. my previous instructions are OK, it’s just the filename that changes?

ThijsDhollander · December 14, 2016, 9:08am

Yep, the format in the file itself is exactly the same! (and you can also still include multiple schemes in one file, as long as none share the same number of directions)

gmkerbler · December 15, 2016, 6:31am

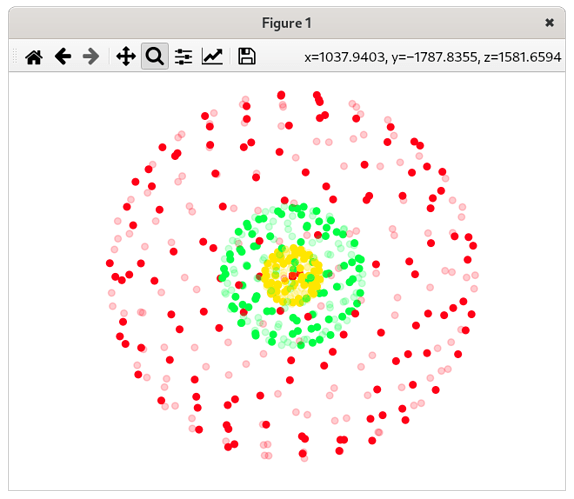
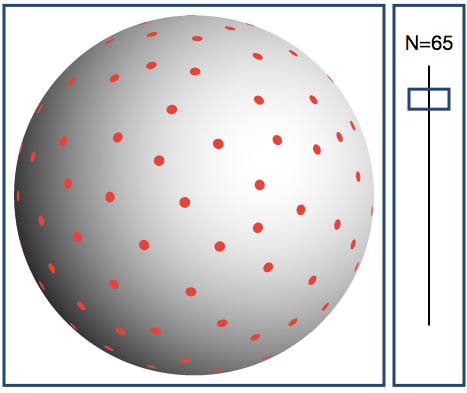
I looked up Caruyer’s web tool (Q Space sampling in Diffusion MRI Emmanuel Caruyer homepage — CNRS Researcher, Univ Rennes, Inria, CNRS, IRISA (UMR 6074), Empenn ERL 1228, Rennes FR-35042.), selecting a single shell, 65 samples and the rightmost option for ‘Number of points per shell’ as it seems as the most equally spaced distribution to me, gives these vectors:

1    0.049    -0.919    -0.391
1    0.726    0.301    -0.618
1    -0.683    0.255    -0.684
1    0.845    -0.502    -0.186
1    -0.730    -0.619    -0.288
1    -0.051    0.039    0.998
1    -0.018    0.871    -0.491
1    -0.444    0.494    0.747
1    -0.989    -0.086    -0.116
1    -0.470    -0.855    0.221
1    0.412    0.400    0.819
1    -0.552    0.790    -0.267
1    -0.123    -0.477    0.871
1    -0.848    0.141    0.510
1    -0.341    -0.788    -0.512
1    0.361    -0.529    0.768
1    -0.472    0.850    0.234
1    -0.856    -0.481    0.189
1    0.797    0.162    0.582
1    0.467    -0.009    -0.884
1    0.013    0.998    -0.056
1    0.882    -0.387    0.267
1    0.017    -0.536    -0.844
1    -0.442    -0.651    0.617
1    0.365    -0.058    0.929
1    0.977    -0.004    -0.213
1    -0.406    -0.902    -0.145
1    -0.627    0.614    0.479
1    -0.354    0.772    -0.528
1    -0.658    -0.472    -0.586
1    0.423    0.322    -0.847
1    0.212    -0.754    -0.622
1    0.912    -0.104    0.398
1    -0.311    0.947    -0.077
1    0.679    0.632    -0.374
1    0.135    -0.286    0.949
1    -0.647    0.230    0.727
1    0.904    0.397    0.158
1    -0.757    0.647    -0.087
1    0.143    0.284    0.948
1    0.233    0.894    -0.382
1    0.664    -0.531    0.527
1    0.157    0.710    0.686
1    -0.895    -0.214    0.392
1    0.594    0.080    0.801
1    -0.006    0.688    -0.726
1    0.665    0.746    0.024
1    -0.277    0.276    0.920
1    -0.962    0.268    0.046
1    -0.133    -0.970    -0.202
1    0.790    -0.405    -0.461
1    -0.194    -0.193    0.962
1    -0.236    0.952    0.195
1    -0.884    -0.272    -0.379
1    0.463    -0.307    0.831
1    0.700    0.066    -0.711
1    -0.200    0.928    -0.314
1    0.550    0.705    0.449
1    -0.670    0.727    0.153
1    0.237    0.722    -0.650
1    0.960    0.260    -0.100
1    0.407    -0.756    -0.512
1    -0.355    -0.180    -0.917
1    -0.809    0.324    -0.491
1    -0.281    -0.955    0.096

In the visualisation window of the web application itself it looks like the samples are not equally spaced, with areas containing big gaps and others seem oversampled - is this what you refer to as ‘angular bias’ @ThijsDhollander? It definitely doesn’t look as bad as the directions I somehow ended up with though…

Here is a multi-shell acquisition scheme generated with gen_scheme.sh and then modified with @jdtournier’s scaling method:

$ cat dw_scheme_SIEMENS.txt 
[directions=106]
CoordinateSystem = xyz
Normalisation = none

Vector[1] = ( 0, 0, 0 )
Vector[2] = ( -0.85835, 0.351655, 0.373597 )
Vector[3] = ( 0.521889, -0.236879, -0.0696683 )
Vector[4] = ( 0.52077, 0.412496, 0.747426 )
Vector[5] = ( 0.241151, 0.802467, -0.545796 )
Vector[6] = ( -0.251295, -0.35357, -0.381015 )
Vector[7] = ( 0.276752, -0.937285, -0.211907 )
Vector[8] = ( 0.242396, -0.035459, -0.969529 )
Vector[9] = ( -0.00197281, -0.29558, 0.495945 )
Vector[10] = ( 0.759659, -0.328221, 0.561417 )
Vector[11] = ( -0.952524, -0.304419, 0.00528 )
Vector[12] = ( 0.32648, 0.453848, -0.144104 )
Vector[13] = ( -0.328866, -0.878423, -0.346729 )
Vector[14] = ( 0, 0, 0 )
Vector[15] = ( 0.170783, -0.458375, 0.872196 )
Vector[16] = ( -0.231188, 0.14737, 0.508102 )
Vector[17] = ( -0.361395, 0.593068, 0.719489 )
Vector[18] = ( -0.72093, -0.480617, 0.499267 )
Vector[19] = ( -0.151375, 0.546899, -0.106395 )
Vector[20] = ( 0.577098, -0.786415, 0.220247 )
Vector[21] = ( -0.599497, -0.796171, 0.08195 )
Vector[22] = ( -0.442197, 0.0153425, -0.37089 )
Vector[23] = ( -0.929851, 0.26932, -0.250687 )
Vector[24] = ( 0, 0, 0 )
Vector[25] = ( 0.185826, 0.353682, 0.916721 )
Vector[26] = ( -0.456234, -0.243143, 0.257032 )
Vector[27] = ( 0.724463, -0.187154, -0.66342 )
Vector[28] = ( -0.02136, 0.934291, -0.355871 )
Vector[29] = ( 0.122686, -0.543696, -0.150585 )
Vector[30] = ( 0.896217, 0.283163, 0.341488 )
Vector[31] = ( -0.32872, 0.162867, -0.930278 )
Vector[32] = ( 0.565321, 0.0441107, 0.108629 )
Vector[33] = ( 0.572133, 0.33085, -0.750468 )
Vector[34] = ( 0, 0, 0 )
Vector[35] = ( -0.795972, 0.605333, -0.00049 )
Vector[36] = ( -0.0114304, 0.00992465, -0.577152 )
Vector[37] = ( -0.116376, -0.812885, -0.570679 )
Vector[38] = ( -0.332183, 0.644876, -0.688324 )
Vector[39] = ( 0.360805, -0.276676, 0.355814 )
Vector[40] = ( -0.480141, 0.761116, 0.436082 )
Vector[41] = ( -0.723507, -0.509273, -0.466024 )
Vector[42] = ( -0.00928437, 0.43851, 0.375442 )
Vector[43] = ( 0.907024, 0.271044, -0.322247 )
Vector[44] = ( 0, 0, 0 )
Vector[45] = ( -0.015382, -0.999007, 0.041804 )
Vector[46] = ( -0.439387, 0.206946, 0.312162 )
Vector[47] = ( -0.309117, -0.29173, 0.905174 )
Vector[48] = ( -0.642148, 0.079946, -0.7624 )
Vector[49] = ( -0.365071, -0.431087, -0.119249 )
Vector[50] = ( 0.146449, -0.340902, -0.928622 )
Vector[51] = ( -0.992235, 0.015623, 0.123389 )
Vector[52] = ( -0.0780543, -0.491317, 0.292999 )
Vector[53] = ( 0.330623, 0.942519, 0.048444 )
Vector[54] = ( 0, 0, 0 )
Vector[55] = ( 0.324729, -0.843726, 0.427407 )
Vector[56] = ( 0.416091, 0.0335238, -0.398846 )
Vector[57] = ( 0.549753, 0.735968, -0.395122 )
Vector[58] = ( 0.725418, -0.619807, -0.299347 )
Vector[59] = ( 0.261234, 0.12145, 0.50034 )
Vector[60] = ( 0.136728, 0.555997, -0.819862 )
Vector[61] = ( 0.819466, 0.556618, 0.136569 )
Vector[62] = ( 0.376063, -0.42012, 0.124133 )
Vector[63] = ( -0.455343, 0.301168, 0.837831 )
Vector[64] = ( -0.869446, 0.033431, -0.492896 )
Vector[65] = ( 0.258842, 0.337401, -0.390506 )
Vector[66] = ( -0.260754, -0.601423, -0.75518 )
Vector[67] = ( 0, 0, 0 )
Vector[68] = ( 0.092766, 0.070563, 0.993184 )
Vector[69] = ( 0.247737, -0.370588, -0.366912 )
Vector[70] = ( -0.587498, 0.62069, -0.51922 )
Vector[71] = ( -0.776311, -0.147095, 0.612947 )
Vector[72] = ( 0.512602, 0.265504, -0.00898068 )
Vector[73] = ( 0.026477, 0.960997, 0.275288 )
Vector[74] = ( 0.94268, -0.327347, -0.064795 )
Vector[75] = ( 0.146068, 0.523886, 0.193754 )
Vector[76] = ( -0.296275, 0.948029, -0.116026 )
Vector[77] = ( 0, 0, 0 )
Vector[78] = ( 0.480945, 0.686288, 0.54562 )
Vector[79] = ( -0.218841, 0.146305, -0.513845 )
Vector[80] = ( -0.437664, -0.138064, -0.888475 )
Vector[81] = ( -0.429632, -0.594218, 0.679942 )
Vector[82] = ( -0.516157, 0.191299, -0.174125 )
Vector[83] = ( 0.191135, -0.82689, -0.528886 )
Vector[84] = ( 0.508971, -0.381313, 0.771718 )
Vector[85] = ( -0.356345, 0.434254, 0.133323 )
Vector[86] = ( 0.636227, -0.489432, -0.596382 )
Vector[87] = ( 0, 0, 0 )
Vector[88] = ( 0.801218, 0.566919, -0.19145 )
Vector[89] = ( -0.555695, -0.0108975, 0.156262 )
Vector[90] = ( -0.301232, -0.918303, 0.256864 )
Vector[91] = ( 0.734823, 0.212395, 0.644145 )
Vector[92] = ( -0.167418, 0.431686, -0.344893 )
Vector[93] = ( -0.536691, -0.018202, 0.843583 )
Vector[94] = ( 0.789658, -0.536403, 0.297845 )
Vector[95] = ( -0.0185907, -0.240673, -0.524466 )
Vector[96] = ( 0.050264, -0.760865, 0.646961 )
Vector[97] = ( 0, 0, 0 )
Vector[98] = ( -0.058902, 0.613791, 0.787268 )
Vector[99] = ( 0.453892, 0.227329, 0.275021 )
Vector[100] = ( 0.908465, -0.053289, -0.414551 )
Vector[101] = ( -0.606147, -0.759705, -0.235446 )
Vector[102] = ( -0.106733, -0.565394, 0.0476504 )
Vector[103] = ( 0.012244, 0.227929, -0.973601 )
Vector[104] = ( 0.553153, -0.827272, -0.098197 )
Vector[105] = ( -0.210825, -0.123454, 0.523111 )
Vector[106] = ( -0.982952, -0.026558, -0.181936 )

Does this have the desired scaling? (Thanks for the code!)

I checked with the scan operators, and the free mode is available (they purchased the license). I’m still a bit puzzled as to why a true multi-shell acquisition wasn’t performed, but instead two separate single shells.
Also the data coming off the scanner always has all the b0’s as the very first images, followed by the diffusion-weighted images, but with regards to using TOPUP later on, a stack of b0’s at the start doesn’t give you any information about the movement and scanner drift throughout the scan, which is what TOPUP uses for its motion correction step if I’m correct?

With regards to the reverse-PE b0 that is acquired as a separate run, I’m guessing there’s no other way than simply using it as an input to TOPUP without doing some sort of rigid/affine alignment to the b0’s of the main run?

jdtournier · December 15, 2016, 9:56am

Yes, it’s better, but still not great. This is what dirstat reports for that set of directions:

dirs65_caruyer.txt [ 65 directions ]

  Bipolar electrostatic repulsion model:
    nearest-neighbour angles: mean = 15.2971, range [ 12.5991 - 18.6859 ]
    energy: total = 9796.37, mean = 150.713, range [ 138.402 - 166.879 ]

  Unipolar electrostatic repulsion model:
    nearest-neighbour angles: mean = 17.7442, range [ 12.8562 - 30.1488 ]
    energy: total = 4822.01, mean = 74.1848, range [ 47.6304 - 105.468 ]

  Spherical Harmonic fit:
    condition numbers for lmax = 2 -> 8: 1.06646 1.1705 1.34612 1.92901

This compares with the equivalent generated with dirgen:

dirs65_dirgen.txt [ 65 directions ]

  Bipolar electrostatic repulsion model:
    nearest-neighbour angles: mean = 17.9718, range [ 17.6542 - 18.6834 ]
    energy: total = 9566.84, mean = 147.182, range [ 146.039 - 148.414 ]

  Unipolar electrostatic repulsion model:
    nearest-neighbour angles: mean = 18.9825, range [ 17.6542 - 35.4085 ]
    energy: total = 4844.27, mean = 74.5273, range [ 40.5906 - 97.0629 ]

  Spherical Harmonic fit:
    condition numbers for lmax = 2 -> 8: 1.00996 1.01748 1.02898 1.10564

Note condition number of l_max=8 fit is 1.1 (dirgen) vs. 1.9 (Caruyer). Better than 12 (!), but still not the best you could do. The nearest-neighbour angles are also not as wide as they could be.

Looking at that website though, you can see why these directions aren’t optimal: as you modify the number of directions (that slider on the right of the graphic), you can see that what happens is a process of selection from a larger (presumably itself optimal) set, with no further attempt at updating these directions. As you increase the number, new points appear, but the existing ones don’t budge, and vice-versa. Clearly these directions are not being optimised for that specific number of directions.

I haven’t checked these numbers, but if you’ve used the command I posted previously, I don’t anticipate any particular issues. What I would recommend though is to acquire some data on a phantom, preferably something slow diffusing like an oil phantom, and verify that the log-signal vs b-value decay curve matches with expectation, both in terms of the estimated ADC, and especially in terms of the linearity of the relationship. That’s probably the only way to be completely sure that the b-value scaling as applied is correct. I suppose you could just take our word for it, but we’re not taking responsibility if our advice turns out to be bogus…

Good to hear.

Well, really it’s EDDY that performs the motion correction. TOPUP includes motion correction to make sure its field estimation is minimally affected by motion, but that’s it. I don’t think it makes a great deal of difference to either of them whether the b=0 volumes come first or interspersed, but I would recommend interspersed to minimise the chance of bias between the b=0 and b>0 volumes.

I think that’s correct - depends what you mean by ‘doing some sort of rigid/affine alignment’. Yes, these need to be acquired separately at the moment, but no, you shouldn’t need to do anything to them particularly to use them with TOPUP. I recommend you use the dwipreproc script for this anyway, it should take care of most issues for you.

ThijsDhollander · December 21, 2016, 2:06am

Yes, more or less: what I meant was that data acquired like this will result in biases in the fit (of any model), indeed because certain areas being more or less densely sampled relative to each other. But as @jdtournier mentioned, these sets are clearly not optimal; they can’t be, since they’re not optimised for the selected N: they seem to just be subsets of another fixed set. Let’s say for some N you would have a reasonable scheme in that tool, then going for N+1 can’t do anything else than result in a much denser sampling exactly where that extra direction is put… Same thing the other way around when going for N-1: it can only result in a certain area suddenly being undersampled. I wasn’t fully aware that this is how that tool behaved… but taking this now into account, I would recommend against using it. @jdtournier’s instructions should give you a good (much better) result.

pinghongyeh · December 23, 2016, 7:24am

Hello,

I’d just like to follow up this thread because we are going to implement the multi-shell protocol soon.

First, where can i find the gen_scheme.sh script? It is not in the
I tested the multi-shell scheme created by using Caruyer’s web tool. It appears that is problematic of that tool. Now, I would like to use the HCP 3 shells (b=1000, 2000, 3000 with 90 directions for each shell) as the gold standard.
Does anyone have the vector table handy that can be shared? Any comment on HCP multi-shell scheme?
The 3D vectors display is cool. Are those scripts available too (black and white display is fine)

Thanks.

Ping

ThijsDhollander · December 23, 2016, 8:04am

Was about to leave work for the holidays now, but I’ll quickly chip in with what I can:

That one of Donald’s scripts; I’m sure he can provide you with it, but I think it’s indeed not (yet?) in MRtrix3 publicly.
So: yes, given what I’ve seen now, I wouldn’t advice to use that webtool to be honest. The HCP scheme is certainly fine if you can run it, but it may be (lots of) overkill… If you want to be a bit more economic, go for (a lot) less directions specifically on the lower b-value’d shells. And even go for one less shell. Like b = 0,1000,3000 with 6,20,60 images/directions.
Here’s the code from what I quickly wrote and use myself at times. It’s quite simple really:

function showdirs(dirs)
%SHOWDIRS shows a set of directions.
%
%   SHOWDIRS(dirs) shows the N directions provided by the N-by-3 matrix
%   dirs and allows instant rotation using the arrow keys or mouse.
%   The provided directions are shown as green filled circles, their
%   opposites as red asterisks.
%
%   Originally written by Thijs Dhollander (24/02/2015)

 figure('color','k'); hold on; axis off;
 [X,Y,Z] = sphere(42);
 surf(X*0.98,Y*0.98,Z*0.98,'FaceColor','blue','FaceLighting','gouraud','SpecularStrength',0,'LineStyle','none');
 
 nn = hypot(hypot(dirs(:,1),dirs(:,2)),dirs(:,3));
 dirsn = dirs./repmat(nn,1,3);
 scatter3(dirsn(:,1),dirsn(:,2),dirsn(:,3),'go','filled');
 scatter3(-dirsn(:,1),-dirsn(:,2),-dirsn(:,3),'r*');
 
 axis([-1 1 -1 1 -1 1]); axis vis3d;
 view(0,0); camlight(45,45);
 rotate3d;

end

Simply copy-paste and save as showdirs.m somewhere in a folder that is in your Matlab path. Works on an N by 3 matrix of xyz coordinates of directions. Even normalises them for you if they weren’t normalised already.

I’ve created an issue in our GitHub (where we develop MRtrix3) to maybe in the future create a dirview (like mrview and shview) that gives you this kind of visualisation. I can see how something like that can be a simple but really handy tool for certain users and jobs!

Well, Merry Christmas and a Happy New Year everyone. Enjoy your holidays!

jdtournier · December 23, 2016, 2:46pm

OK, by popular request, I’ve just committed the gen_scheme script. It should hopefully land on master within an hour or so…

ros · October 26, 2020, 11:03am

Hi @jdtournier, @ThijsDhollander . Is there a way to visualize multi shell sequences in the sphere, with different vector lengths for each b-values?
I mean something like this
I have a 3-shell sequence but with show_dirs code I guess the three shells’ gradient directions are on the same surface

thanks
Rosella

jdtournier · October 27, 2020, 3:48pm

OK, this comes up often enough that I’ve cobbled together a quick Python script to do this. You’ll find it here, and reproduced below. This is what it produces for the dHCP acquisition, for example:

Code:

#!/usr/bin/python

opacity_of_negative_direction = 0.2
size_of_markers = 30
range_of_b = [0.0, 1.0e99]
colormap = 'hsv'

import matplotlib.pyplot as plt
import numpy as np
import sys

data = np.loadtxt (sys.argv[1])
bmax = np.max(data[:,3])
n = [ i for i in np.arange(len(data)) if data[i,3] >= range_of_b[0] and data[i,3] <= range_of_b[1] ]

b = data[n,3]
data = data[n,0:3] * np.reshape (b, (-1,1))

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

ax.scatter ( data[:,0],  data[:,1],  data[:,2],
    vmin=0, vmax=bmax, c=b, s=size_of_markers,
    alpha=1.0, cmap=plt.get_cmap(colormap))
ax.scatter (-data[:,0], -data[:,1], -data[:,2],
    vmin=0, vmax=bmax, c=b, s=size_of_markers,
    alpha=opacity_of_negative_direction, cmap=plt.get_cmap(colormap))

ax.set_box_aspect([1, 1, 1])
ax.set_position([0, 0, 1, 1])
ax.set_axis_off()
plt.show()

maxpietsch · October 27, 2020, 4:57pm

This might not work on newer versions of matplotlib (see here). If anyone has a workaround, I’d like to know. Currently, I am using mayavi, below code runs in a jupyter notebook and should be easy to adapt to multi-shell data:

from mayavi import mlab
mlab.init_notebook()
import numpy as np

def render_sphere():
    """ Create a sphere """
    r = 1.0
    pi = np.pi
    cos = np.cos
    sin = np.sin
    phi, theta = np.mgrid[0:pi:101j, 0:2 * pi:101j]

    x = r*sin(phi)*cos(theta)
    y = r*sin(phi)*sin(theta)
    z = r*cos(phi)

    mlab.figure(1, bgcolor=(1, 1, 1), fgcolor=(0, 0, 0), size=(400, 300))
    mlab.clf()

    # sphere
    mlab.mesh(x , y , z, color=(0.5,0.5,0.5), opacity=1)

def render_points(bvecs, color=(1.0,0,1.0), color2=(0.0,1.0,0.0)):
    """ Render points as small spheres """
    if bvecs is None:
        data = np.random.randn(20,3)
    elif type(bvecs) is np.ndarray:
        data = bvecs.copy()
    else:
        data = np.loadtxt(bvecs).T
    norm = np.sqrt((data**2).sum(1))[:,None]
    norm[norm==0] = 1
    data /= norm
    p = mlab.points3d(*np.hsplit(data, 3), scale_factor=0.05, color=color)
    if color2 is None:
        return p
    return mlab.points3d(*np.hsplit(-data, 3), scale_factor=0.05, color=color2)

render_sphere()
r = render_points(fsl_bvec, color=(1,1,1), color2=(0,0,0))
r

jdtournier · October 27, 2020, 5:05pm

This is why I’m using set_box_aspect(), not set_aspect('equal'). This works fine on matplotlib 3.3.2 (the latest right now).

maxpietsch · October 27, 2020, 7:51pm

Yes, you are right, I mistook set_box_aspect for set_aspect. Since matplotlib 3.3 set_box_aspect exists and does the job. I tested on 3.2.1 where set_aspect, which used to work in earlier versions (in specific scenarios), caused an error. Glad this feature hole is finally solved.

ros · November 12, 2020, 12:54pm

Thank you for solving the issue. I hust have a question: how should the txt file with direction scheme be like?
thank you
Rosella